Plus Two Maths Chapter 12 Linear Programming Chapter Wise Question and Answers PDF Download: Students of Standard 12 can now download Plus Two Maths Chapter 12 Linear Programming chapter wise question and answers pdf from the links provided below in this article. Plus Two Maths Chapter 12 Linear Programming Question and Answer pdf will help the students prepare thoroughly for the upcoming Plus Two Maths Chapter 12 Linear Programming exams.
Plus Two Maths Chapter 12 Linear Programming Chapter Wise Question and Answers
Plus Two Maths Chapter 12 Linear Programming question and answers consists of questions asked in the previous exams along with the solutions for each question. To help them get a grasp of chapters, frequent practice is vital. Practising these questions and answers regularly will help the reading and writing skills of students. Moreover, they will get an idea on how to answer the questions during examinations. So, let them solve Plus Two Maths Chapter 12 Linear Programming chapter wise questions and answers to help them secure good marks in class tests and exams.
|
Board |
Kerala Board |
|
Study Materials |
Chapter wise Question and Answers |
|
For Year |
2021 |
|
Class |
12 |
|
Subject |
Mathematics |
|
Chapters |
Maths Chapter 12 Linear Programming |
|
Format |
|
|
Provider |
How to check Plus Two Maths Chapter 12 Linear Programming Question and Answers?
- Visit our website - https://spandanamblog.com
- Click on the 'Plus Two Question and Answers'.
- Look for your 'Plus Two Maths Chapter 12 Linear Programming Question and Answers'.
- Now download or read the 'Class 12 Maths Chapter 12 Linear Programming Question and Answers'.
Plus Two Maths Chapter 12 Linear Programming Question and Answers PDF Download
We have provided below the question and answers of Plus Two Maths Chapter 12 Linear Programming Chapter wise study material which can be downloaded by you for free. These Plus Two Maths Chapter 12 Linear Programming Chapter Wise Question and answers will contain important questions and answers and have been designed based on the latest Plus Two Maths Chapter 12 Linear Programming, books and syllabus. You can click on the links below to download the Plus Two Maths Chapter 12 Linear Programming Chapter Wise Question and Answers PDF.
Question 1.
Solve the following LPP Graphically;
Maximise; Z = 60x + 15y
Subject to constraints;
x + y ≤ 50, 3x + y ≤ 90, x ≥ 0, y ≥ 0.
Answer:
1. In the figure the shaded region OABC is the fesible region. Here the region is bounded. The corner points are O(0, 0), A(30, 0), B(20, 30), C(0, 50).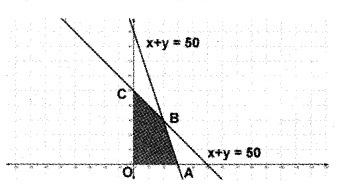
Given; Z = 60x + 15y
| Corner points | Value of Z |
| O | Z = 0 |
| A | Z = 60(30) + 15(0) = 1800 |
| B | Z = 60(20) + 15(30) = 1650 |
| C | Z = 60(0) + 15(50) = 750 |
Since maximum value of Z occurs at A, the soluion is Z = 1800, (30, 0).
Question 2.
Solve the following LPP Graphically;
Minimise; Z = -3x + 4y
Subject to constraints;
x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0
Answer:
In the figure the shaded region OABC is the fesible region. Here the region is bounded. The corner points are O(0, 0), A(4, 0) B(2, 3), C(0, 4).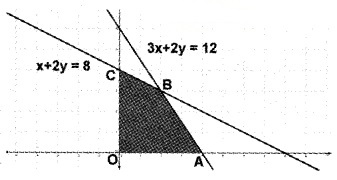
Given; Z = -3x + 4y
| Corner points | Value of Z |
| O | Z = 0 |
| A | Z = -3(4) + 4(0) = -12 |
| B | Z = -3(2) + 4(3) = 6 |
| C | Z = -3(0) + 4(4) = 16 |
Since minimum value of Z occurs at A, the soluion is Z = -12, (4, 0).
Question 3.
Solve the following LPP Graphically;
Maximise; Z = 3x + 5y
Subject to constraints;
x + 3y ≥ 3, x + y ≥ 2, x ≥ 0, y ≥ 0
Answer:
In the figure the shaded region ABC is the fesible region. Here the region is unbouded.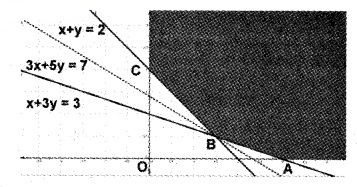
The corner points are A(3, 0), B\(\left(\frac{3}{2}, \frac{1}{2}\right)\), C(0, 2)
Given; Z = 3x + 5y
| Corner points | Value of Z |
| A | Z = 3(3) + 5(0) = 9 |
| B | Z = 3\(\left(\frac{3}{2}\right)\) + 5\(\left(\frac{1}{2}\right)\) = 7 |
| C | Z = 3(0) + 5(2) = 10 |
Form the table, minumum value of Z is 7 at B\(\left(\frac{3}{2}, \frac{1}{2}\right)\). The feasible region is unbounded, so consider the inequality 3x + 5y < 7. Clearly the feasible region has no common points with 3x + 5y < 7, Thus minimum value of Z occurs at B, the soluion is Z = 7.
Plus Two Maths Linear Programming Six Mark Questions and Answers
Question 1.
One kind of a cake requires 200g of flour and 25g of fat, and another kind of cake requires 100g of flour and 50g of fat. Find the maximum number of cakes which can be made from 5kg of flour and 1kg of fat assuming that there is no shortage of the other ingredients, used in making the cake.
Answer:
Let the number of cakes made of type I are x and that of type II are y. Then the total number of cakes will be Z = x + y
Flour constraint 200x + 100y ≤ 5000
Fat constraint 25x + 50y ≤ 1000
Therefore;
Maximise; Z = x + y
2x + y ≤ 50; x + 2y ≤ 40; x ≥ 0, y ≥ 0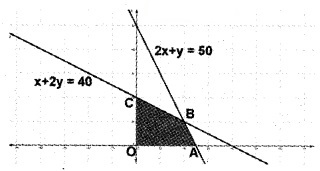
In the figure the shaded region OABC is the feasible region. Here the region is bounded. The corner points are O(0, 0), A(25, 0), B(20, 10), C(0, 20)
Given; Z = x + y
| Corner points | Value of Z |
| O | Z = 0 |
| A | Z = 25 + 0 = 25 |
| B | Z = 20 + 10 = 30 |
| C | Z = 0 + 20 = 20 |
Since maximum value of Z occurs at B, the soluion is Z = 30, (20, 10).
Question 2.
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine and 3hours of craftman’s time in its making, while a cricket bat takes 3 hours of machine time and 1 hour of craftman’s time. In a day, the factory has availability of not more than 42 hours of machine time and 24 hours of craftman’s time.
- What no. of rackets and bats must be produced if the factory is to work at full capacity?
- If the profit on a racket and a bat is 10 find maximum profit.
Answer:
Let the number of rackets made = x and that of bats = y.
Maximise; Z = x + y
Machine constraints 1.5x + 3y ≤ 42
Craftsman’s constraint 3x + y ≤ 24
Therefore; Maximise; Z = x + y
x + 2y ≤ 14, 3x + y ≤ 24, x ≥ 0, y ≥ 0
In the figure the shaded region OABC is the fesible region. Here the region is bounded. The corner points are O(0, 0), A(8, 0), B(4, 10), C(0, 14).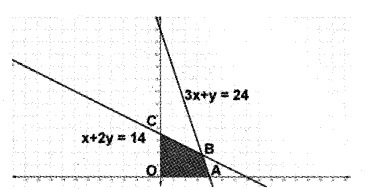
Given; Z = x + y
| Corner points | Value of Z |
| O | Z = 0 |
| A | Z = 8 + 0 = 8 |
| B | Z = 4 + 12 = 16 |
| C | Z = 0 + 14 = 14 |
Since maximum value of Z occurs at B, the soluion is Z = 16, (4, 12).
Question 3.
Two godowns A and B have grains capacity of 100 quintals and 50 quintals respectively. They supply to 3 ration shops D, E, and F whose requirement are 60, 50 and 40 quintals respectively. The cost of transportation per quintal from the godowns to the shops is given in the following table; Transportation cost per quintal(in Rs.)
Hence should the supplies be transported in order that the transportation cost is minimum? What is the minimum cost?
Answer: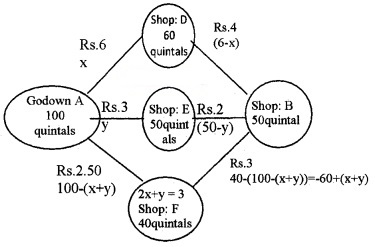
Express the problem diagrammatically as shown above. The total transportation cost is given by
Z = 6x + 3y + 2.5{100 - (x + y)} + 4(60 - x) + 2(50 - y) + 3(-60 + (x + y))
⇒ Z = 2.5x + 1.5y + 410
100 - (x + y) ≥ 0 ⇒ x + y ≤ 100
60 - x ≥ 0 ⇒ x ≤ 60
50 - y ≥ 0 ⇒ y ≤ 50 - 60 + x + y ≥ 0 ⇒ x + y ≥ 60
Then the given LPP is
Minimise; Z = 2.5x + 1.5y + 410
x + y ≤ 100, x + y ≥ 60
0 ≤ x ≤ 60, 0 ≤ y ≤ 50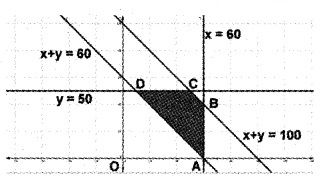
In the figure the shaded region ABCD is the feasible region. Here the region is bounded. The corner points are
A(60, 0), B(60, 40), C(50, 50), D(10, 50).
Given; Z = 2.5x + 1.5y + 410
| Corner points | Value of Z |
| A | Z = 2.5(60) + 1.5(0) + 410= 560 |
| B | Z = 2.5(60) + 1.5(40) + 410 = 620 |
| C | Z = 2.5(50) + 1.5(50) + 410 = 610 |
| D | Z = 2.5(10) + 1.5(50) + 410 = 510 |
Since minimum value of Z occurs at D, the soluion is Z = 510.
Question 4.
(i) Choose the correct answer from the bracket. If an LPP is consistent, then its feasible region is always
(a) Bounded
(b) Unbounded
(c) Convex region
(d) Concave region
(ii) Maximize Z = 2x + 3y subject to the constraints x + y ≤ 4, x ≥ 0, y ≥ 0.
Answer:
(i) (c) Convex region.
(ii)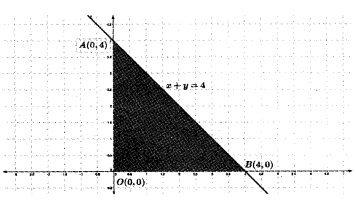
Corner points of the feasible region are as follows
| Corner points | Z = 2x + 3y |
| 0(0, 0) | 0 |
| A(0, 4) | 12 → Maximum |
| B(4, 0) | 8 |
∴ the maximum value of Z is 12 attained at (0, 4).
Question 5.
The graph of a linear programming problem is given below. The shaded region is the feasible region. The objective function is Z = px + qy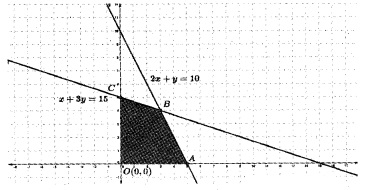
- What are the co-ordinates of the comers of the feasible region.
- Write the constraints
- If the Max. Z occurs at A and B, what is the relation between p and q?
- If q = 1, write the objective function
- Find the Max Z
Answer:
1. Corner points are O(0, 0), A(5, 0), B(3, 4), C(0, 5).
2. Constraints are 2x + y ≤ 10, x + 3y ≤ 15, x ≥ 0, y ≥ 0.
3. At (3, 4), Z = 3p + 4q
At (5, 0), Z = 5p
⇒ 3p + 4q = 5p ⇒ p = 2q.
4. If q = 1, p=2
Then the objective function is,
Maximize Z = 2x + y.
5. At (3, 4) Z = 2 × 3 + 4 = 10 is the maximum value.
Question 6.
A diet is to contain at least 80 units of vitamin A and 100 units of minerals. Two foods F1 and F2 are available. Food F1 costs Rs 4 per unit food and F2 costs Rs 6 per unit. One unit of food F1 contains 3 units of vitamin A and 4 units of minerals. One unit of food F2 contains 6 units of vitamin A and 3 units of minerals. Formulate this as a linear programming problem. Find the minimum costs for diet that consists of mixture of these two foods and also meets the minimal nutritional requirements.
Answer:
Let x units of food F1 and y units of food F2 be in the diet
Total cost Z = 4x + 6y
Then the LPP is
Minimize Z = 4x + 6
Subject to the constraints
3x + 6y ≥ 80
4x + 3y ≥ 100
x, y ≥ 0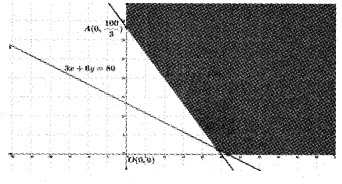
The feasible region is unbounded
Plus Two Mathematics All Chapters Question and Answers
- Plus Two Mathematics Chapter Wise Question and Answers PDF
- Plus Two Maths Chapter 1 Relations and Functions Chapter Wise Question and Answers PDF
- Plus Two Maths Chapter 2 Inverse Trigonometric Functions Chapter Wise Question and Answers PDF
- Plus Two Maths Chapter 3 Matrices Chapter Wise Question and Answers PDF
- Plus Two Maths Chapter 4 Determinants Chapter Wise Question and Answers PDF
- Plus Two Maths Chapter 5 Continuity and Differentiability Chapter Wise Question and Answers PDF
- Plus Two Maths Chapter 6 Application of Derivatives Chapter Wise Question and Answers PDF
- Plus Two Maths Chapter 7 Integrals Chapter Wise Question and Answers PDF
- Plus Two Maths Chapter 8 Application of Integrals Chapter Wise Question and Answers PDF
- Plus Two Maths Chapter 9 Differential Equations Chapter Wise Question and Answers PDF
- Plus Two Maths Chapter 10 Vector Algebra Chapter Wise Question and Answers PDF
- Plus Two Maths Chapter 11 Three Dimensional Geometry Chapter Wise Question and Answers PDF
- Plus Two Maths Chapter 12 Linear Programming Chapter Wise Question and Answers PDF
- Plus Two Maths Chapter 13 Probability Chapter Wise Question and Answers PDF
Benefits of the Plus Two Maths Chapter 12 Linear Programming Chapter Wise Question and Answers PDF
The Plus Two Maths Chapter 12 Linear Programming Chapter Wise Question and Answers PDF that has been provided above is extremely helpful for all students because of the way it has been drafted. It is designed by teachers who have over 10 years of experience in the field of education. These teachers use the help of all the past years’ question papers to create the perfect Plus Two Maths Chapter 12 Linear Programming Chapter Wise Question and Answers PDF.
0 comments:
Post a Comment