Plus Two Maths Chapter 10 Vector Algebra Chapter Wise Question and Answers PDF Download

Plus Two Maths Chapter 10 Vector Algebra Chapter Wise Question and Answers PDF Download: Students of Standard 12 can now download Plus Two Maths Chapter 10 Vector Algebra chapter wise question and answers pdf from the links provided below in this article. Plus Two Maths Chapter 10 Vector Algebra Question and Answer pdf will help the students prepare thoroughly for the upcoming Plus Two Maths Chapter 10 Vector Algebra exams.

Plus Two Maths Chapter 10 Vector Algebra Chapter Wise Question and Answers

Plus Two Maths Chapter 10 Vector Algebra question and answers consists of questions asked in the previous exams along with the solutions for each question. To help them get a grasp of chapters, frequent practice is vital. Practising these questions and answers regularly will help the reading and writing skills of students. Moreover, they will get an idea on how to answer the questions during examinations. So, let them solve Plus Two Maths Chapter 10 Vector Algebra chapter wise questions and answers to help them secure good marks in class tests and exams.

Board	Kerala Board
Study Materials	Chapter wise Question and Answers
For Year	2021
Class	12
Subject	Mathematics
Chapters	Maths Chapter 10 Vector Algebra
Format	PDF
Provider	Spandanam Blog

How to check Plus Two Maths Chapter 10 Vector Algebra Question and Answers?

1. Visit our website - https://spandanamblog.com
2. Click on the 'Plus Two Question and Answers'.
3. Look for your 'Plus Two Maths Chapter 10 Vector Algebra Question and Answers'.
4. Now download or read the 'Class 12 Maths Chapter 10 Vector Algebra Question and Answers'.

Plus Two Maths Chapter 10 Vector Algebra Question and Answers PDF Download

We have provided below the question and answers of Plus Two Maths Chapter 10 Vector Algebra Chapter wise study material which can be downloaded by you for free. These Plus Two Maths Chapter 10 Vector Algebra Chapter Wise Question and answers will contain important questions and answers and have been designed based on the latest Plus Two Maths Chapter 10 Vector Algebra, books and syllabus. You can click on the links below to download the Plus Two Maths Chapter 10 Vector Algebra Chapter Wise Question and Answers PDF. 

Question 1.
Find \(\bar{a}+\bar{b}, \bar{a}-\bar{b}\) and \(\bar{b}+\bar{c}\) using the vectors.
\(\bar{a}\) = 3i + 4j + k, \(\bar{b}\) = 2i – 7 j – 3k and \(\bar{c}\) = 2i + 3j – 9k.
Answer:
\(\bar{a}+\bar{b}\) = 3i + 4j + k + 2i – 7j – 3k = 5i – 3j – 2k
\(\bar{a}-\bar{b}\) = 3i + 4j + k – (2i – 7j -3k) = i + 11j + 4k
\(\bar{b}+\bar{c}\) = 2i – 7j -3k + 2i +3j – 9k
= 4i – 4j – 12k.

Question 2.

1. Find the vector passing through the point A( 1, 2, -3) and B(-1, -2, 1).
2. Find the direction cosines along with AB.

Answer:
1. \(\overline{A B}\) = \(\overline{O B}\) – \(\overline{O A}\) = -i – 2j + k – (i + 2j – 3k) = -2i – 4j + 4k.

2. Unit Vector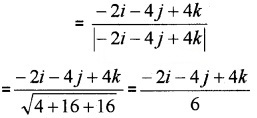

Direction cosines are \(\frac{-2}{6}\), \(\frac{-4}{6}\), \(\frac{4}{6}\).

Question 3.
Show that the points A, B and C with position vectors \(\bar{a}\) = 3i – 4j – 4k, \(\bar{b}\) = 2i – j + k and \(\bar{c}\) = i – 3j – 5k respectively from the vertices of a right angled triangle.
Answer: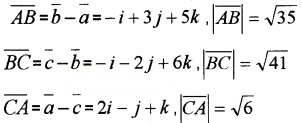

41 = 35 + 6 ⇒ BC² = AB² + CA²
Hence right angled triangle.

Question 4.
Prove that \([\bar{a}+\bar{b} \bar{b}+\bar{c} \bar{c}+\bar{a}]=2[\bar{a} \bar{b} \bar{c}]\).
Answer:
LHS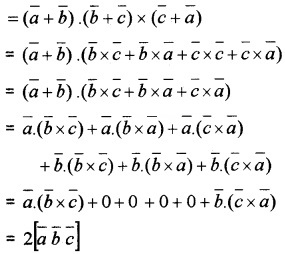

Note: If \(\bar{a}\), \(\bar{b}\), \(\bar{c}\) are coplanar then so is \([\bar{a}+\bar{b} \bar{b}+\bar{c} \bar{c}+\bar{a}]\).

Question 5.
Consider the vector \(\bar{p}\) = 2i – j + k. Find two vectors \(\bar{q}\) and \(\bar{r}\) such that \(\bar{p}\), \(\bar{q}\) and \(\bar{r}\) are mutually perpendicular.
Answer:
Find a vector \(\bar{q}\) such that \(\bar{p} \cdot \bar{q}\) = 0, for this use any \(\bar{q}\) whose two components are randomly selected. Let \(\bar{q}\) = 2i + 2j + xk
\(\bar{p} \cdot \bar{q}\) = (2i – j + k) . (2i + 2 j + xk) = 0
⇒ 4 – 2 + x = 0 ⇒ x = -2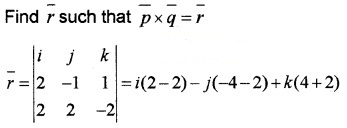

= 6j + 6k.

Question 6.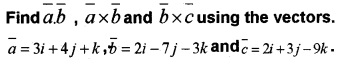

Answer: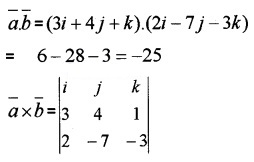

= i(-12 + 7) – j(-9 – 2) + k(-21 – 8)
= -5i + 11j – 29k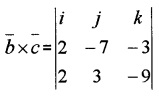

= i(63 + 9) – j(-18 + 6) + k(6 – 14)
= 72i + 12 j – 8k.

Question 7.
If \(\bar{a}\) = 3i + j + 2k,
(i) Find the magnitude of \(\bar{a}\). (1)
(ii) If the projection of \(\bar{a}\) on another vector \(\bar{b}\) is \(\sqrt{14}\), which among the following could be \(\bar{b}\) ? (1)
(a) i + j + k
(b) 6i + 2j + 4k
(c) 3i – j + 2k
(d) 2i + 3j + k
(iii) If \(\bar{a}\) makes an angle 60° with a vector \(\bar{c}\), find the projection of \(\bar{a}\) on \(\bar{c}\) (1)
Answer:

(ii) Since projection of \(\bar{a}\) on another vector \(\bar{b}\) and magnitude of \(\bar{a}\) is \(\sqrt{14}\), then \(\bar{a}\) and \(\bar{b}\) are parallel, (b) 6i + 2j + 4k.

(iii) Projection of \(\bar{a}\) on \(\bar{c}\)
= |\(\bar{a}\)|cos60° = \(\sqrt{14}\) × \(\frac{1}{2}\) = \(\frac{\sqrt{14}}{2}\).

Question 8.
(i) The projection of the vector 2i + 3j + 2k on the vector i + j + k is (1)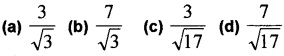

(ii) Find the area of a parallelogram whose adjacent sides are the vectors 2i + j + k and 6i – j (2)
Answer:

(ii) Let \(\bar{a}\) = 2i + j + k, \(\bar{b}\) = i – j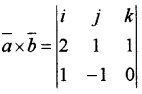

= i(0 + 1) – j(0 – 1) + k(-2 – 1 ) = i + j -3k
Area =

Question 9.
(i) The angle between the vectors i + j and j + k is (1)
(a) 60°
(b) 30°
(c) 45°
(d) 90°

Answer:
(i) (a) 60°

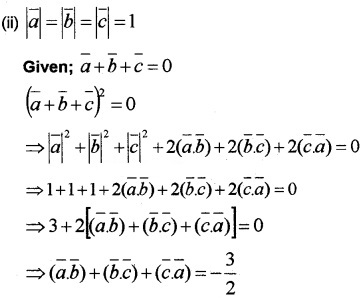
Question 10.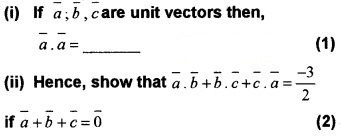

Answer:

(ii) Given, \(\bar{a}\) + \(\bar{b}\) + \(\bar{a}\) = \(\bar{0}\), squaring both sides we get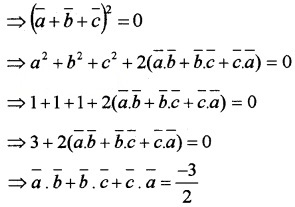

Plus Two Maths Vector Algebra Four Mark Questions and Answers

Question 1.
Let A (2, 3), B (1, 4), C (0, -2), and D (x, y) are vertices of a parallelogram ABCD.

1. Write the position vectors A, B, C, and D. (2)
2. Find the value of x and y. (2)

Answer:
1. Position vector of A = 2i + 3 j
Position vector of B = i + 4j
Position vector of C = 0i – 2j
Position vector of D = xi + yj.

2. Since ABCD is a parallelogram, then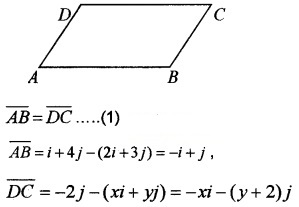

(1) ⇒ -i + j = -xi – (y + 2 )j
x = 1, -2 – y = 1 ⇒ y = -3
∴ D is (1, -3).

Question 2.
Find the position vector of a point R which divides the line joining the two points P and Q whose vectors i + 2j – k and -i + j + k in the ratio 2:1

1. internally and
2. externally.

Answer:
\(\overline{O P}\) = i + 2j – k, \(\overline{O Q}\) = -i + j + k
Let R be the position vector of the dividing point,
1.

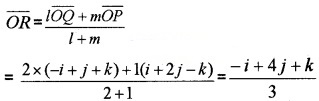
2.

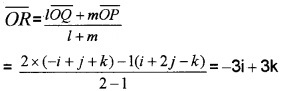
Question 3.
(i) Choose the correct answer from the bracket. If a unit vector \(\widehat{a}\) makes angles \(\frac{\pi}{4}\) with i and \(\frac{\pi}{3}\) with j and acute angle θ with k. then θ is
(a) \(\frac{\pi}{6}\),
(b) \(\frac{\pi}{4}\),
(c) \(\frac{\pi}{3}\),
(d) \(\frac{\pi}{2}\) (1)
(ii) Find a unit vector \(\widehat{a}\) (1)
(iii) Write down a unit vector in XY plane, making an angle 60°of with the positive direction of x – axis. (2)
Answer:
(i) (c), Since I = cos\(\frac{\pi}{4}\) = \(\frac{1}{\sqrt{2}}\), m = cos\(\frac{\pi}{3}\) = 1/2;
n = cos θ
l² + m² + n² = 1
n² = 1 – (\(\frac{1}{2}\))² – (\(\frac{1}{\sqrt{2}}\))² = 1/4
n = \(\frac{1}{2}\), cosθ = 1/2 , θ = \(\frac{\pi}{3}\).

(ii)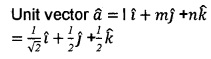

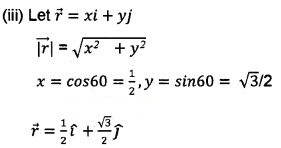
Question 4.
Let the vectors \(\bar{a}\), \(\bar{b}\), \(\bar{c}\) denoted the sides of a triangle ABC.
(i) Prove that (2)

(ii) Find the projection of the vector i + 3j + 7k on the vector 7i – j + 8k (2)
Answer: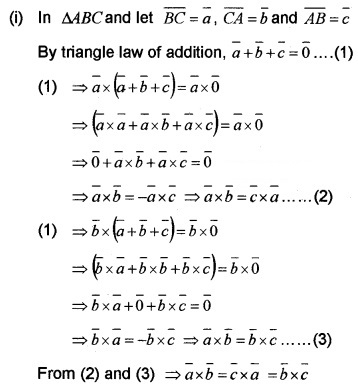

(ii) Projection of the vector i + 3j + 7k on the vector 7i – j + 8k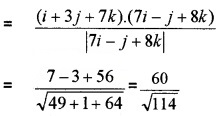

Question 5.
(i) If \(\bar{a}\) and \(\bar{b}\) are any two vectors, then axb is (1)
(a) a vector on the same plane where \(\bar{a}\) and \(\bar{b}\) lie.
(b) ab cosθ, if θ is the angle between them.
(c) a vector parallel to both \(\bar{a}\) and \(\bar{b}\).
(d) a vector perpendicular to both \(\bar{a}\) and \(\bar{b}\).
(ii) Let \(\bar{a}\) = 2i + 4j – 5k, \(\bar{b}\) = i + 2j + 3k. Then find a unit vector perpendicular to both \(\bar{a}\) and \(\bar{b}\). (2)
(iii) Find a vector of magnitude 5 in the direction perpendicular to both \(\bar{a}\) and \(\bar{b}\) (1)
Answer:
(i) (d) a vector perpendicular to both \(\bar{a}\) and \(\bar{b}\).

(ii) \(\bar{a}\) = 2i + 4j-5k, \(\bar{b}\) = i + 2j+3k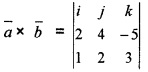

= i(12 + 10) – j(6 + 5) + k(4 – 4) = 22i – 11j

Therefore unit vector perpendicular to both \(\bar{a}\) and \(\bar{b}\) is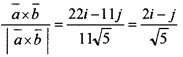

(iii) 5 × unit vector perpendicular to both \(\bar{a}\) and \(\bar{b}\)

Question 6.
Consider a vector that is inclined at an angle 45° to x-axis and 60° to y-axis

1. Find the dc’s of the vector. (2)
2. Find a unit vector in the direction of the above vector. (1)
3. Find a vector which is of magnitude 10 units in the direction of the above vector. (1)

Answer:
1. Let l, m, n are the direction ratios.
Given that, l = cos 45° = \(\frac{1}{\sqrt{2}}\), m = cos 60° = \(\frac{1}{2}\)
⇒ l² + m² + n² = 1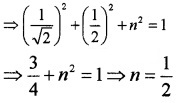

∴ the dc’s of the vector are \(\frac{1}{\sqrt{2}}\), \(\frac{1}{2}\), \(\frac{1}{2}\)

2. A unit vector in the direction of the above vector is given by li + mj + nk ⇒ \(\frac{1}{\sqrt{2}}\)i + \(\frac{1}{2}\)j + \(\frac{1}{2}\)k.

3. A vector, which is of magnitude 10 units in the direction of the above vector is given by

Question 7.
Consider the point A(2, 1, 1) and B(4, 2, 3)

1. Find the vector \(\overline{A B}\) (1)
2. Find the direction cosines of \(\overline{A B}\) (2)
3. Find the angle made by \(\overline{A B}\) with the positive direction of x-axis. (1)

Answer:
1. \(\overline{A B}\) = 2i + j + 2k

2. |\(\overline{A B}\)| = \(\sqrt{4+1+4}\) = 3
The direction cosines are \(\frac{2}{3}\), \(\frac{1}{3}\), \(\frac{2}{3}\).

3. cos α = \(\frac{2}{3}\) ⇒ α = cos^-1(\(\frac{2}{3}\)).

Question 8.
If i + j + k, 2i + 5j, 3i + 2 j – 3k, i – 6j – k respectively are the position vector of points A, B,C and D. Then

1. Find \(\overline{A B}\) and \(\overline{C D}\). (1)
2. Find the angle between the vectors \(\overline{A B}\) and \(\overline{C D}\). (2)
3. Deduce that \(\overline{A B}\) parallel to \(\overline{C D}\). (1)

Answer:
1.

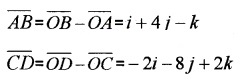
2.

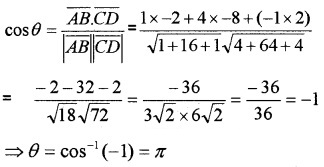
3. Since the angle between \(\overline{A B}\) and \(\overline{C D}\) is π they are parallel.

Question 9.
Let ABCD be a parallelogram with sides as given in the figure.

1. Find area of the parallelogram. (2)
2. Find the distance between the sides AB and DC. (2)

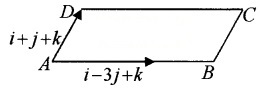
Answer:
1. Given;
\(\overline{A B}\) = i – 3j + k and \(\overline{A D}\) = i + j + k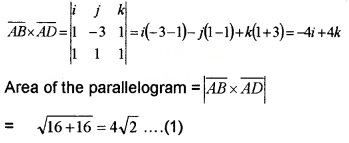

2. Let h be the distance between the parallelsides AB and DC. Then ; Area = Base × h _____(2)
Here, Base = |\(\overline{A B}\)|
|i – 3j + k| = \(\sqrt{1+9+1}=\sqrt{11}\)
From (1) and (2)

Question 10.
Consider \(\bar{a}\) = i + 2j – 3k, \(\bar{b}\) = 3i – j + 2k, \(\bar{c}\) = 11i + 2j

1. Find \(\bar{a}\) + \(\bar{b}\) and \(\bar{a}\).\(\bar{b}\) (2)
2. Find the unit vector in the direction of \(\bar{a}\) + \(\bar{b}\). (1)
3. Show that \(\bar{a}\) + \(\bar{b}\) and \(\bar{a}\) – \(\bar{b}\) are orthogonal. (1)

Answer: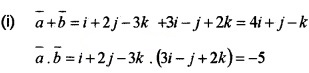

(ii) Unit vector in the direction of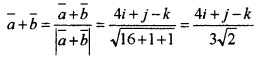

(iii) We have,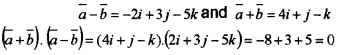

Therefore, they are orthogonal.

Question 11.
Let A (1, -1, 4), B ( 2, 1, 2 ) and C (1, -2, -3 )

1. Find \(\overline{A B}\). (1)
2. Find the angle between \(\overline{A B}\) and \(\overline{A C}\).(2)
3. Find the area of the parallelogram formed by \(\overline{A B}\) and \(\overline{A C}\) as adjacent sides. (1)

Answer:
1. \(\overline{A B}\) = P.v of B – P.v of A
= 2 i + j + 2 k – (i – j + 4k) = i + 2 j – 2k

2. \(\overline{A C}\) = P.v of C – P.v of A
= i – 2 j – 3 k -(i – j + 4k) = – j – 7k
Let A be the angle between \(\overline{A B}\) and \(\overline{A C}\)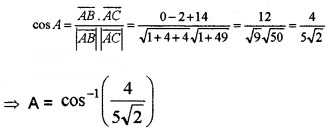

3.

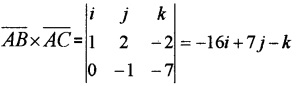
Area of the parallelogram

Plus Two Maths Vector Algebra Six Mark Questions and Answers

Question 1.
Using this figure answer the following questions.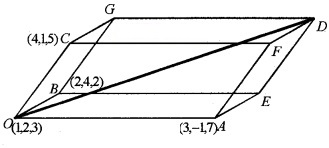

1. Find \(\overline{O A}\), \(\overline{O B}\), \(\overline{O C}\) (2)
2. Find \(\overline{O D}\) (2)
3. Find the coordinate of the vertex D. (2)

Answer:
1. \(\overline{O A}\) = (3 – 1)i + (-1 – 2)j + (7 – 3)k = 2i – 3j + 4k
\(\overline{O B}\) = (2 – 1)i + (4 – 2)j +(2 – 3)k = i + 2j – k
\(\overline{O C}\) = (4 – 1)i + (1 – 2 )j + (5 – 3 )k = 3i – j + 2 k.

2. From the figure,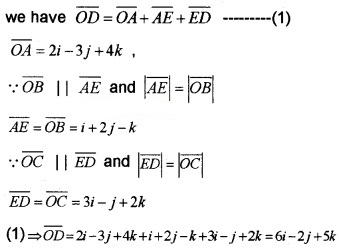

3. Let the vertex of D be (x , y , z),
Then, \(\overline{O D}\) = (x – 1)i + (y – 2)j + (z – 3)k.
But we have,
\(\overline{O D}\) = 6i – 2j + 5k = (x – 1)i + (y – 2)j +(z – 3)k
x – 1 = 6 ⇒ x = 7, y – 2 = -2 ⇒ y = 0, z – 3 = 5 ⇒ z = 8.

Question 2.
OABCDEFG is a cube with edges of length 8 units and axes as shown. L, M, N are midpoints of the edges FG, GD, GB respectively.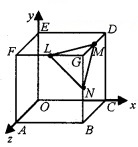

1. Find p.v’s of F, B,D and G. (1)
2. Show that the angle between the main diagonals is θ = cos^-1\(\left(\frac{1}{3}\right)\). (2)
3. Find the p.v’s of L, M, N. (1)
4. Show that \(\overline{L M}+\overline{M N}+\overline{N L}=0\). (1)

Answer:
1. \(\overline{O F}\) = 8 j + 8k, \(\overline{O B}\) = 8i + 8k, \(\overline{O D}\) = 8i + 8k, \(\overline{O G}\) = 8i + 8j + 8k.

2. Consider the main diagonals \(\overline{O G}\) and \(\overline{E B}\)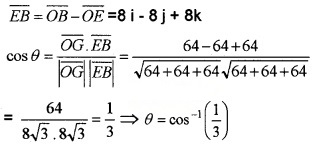

3. P.V of L = \(\overline{O L}\) = 4i + 8j + 8k
P.V of M = \(\overline{O M}\) = 8i + 8j + 4k
P.V of N = \(\overline{O N}\) = 8i + 4j + 8k

4.

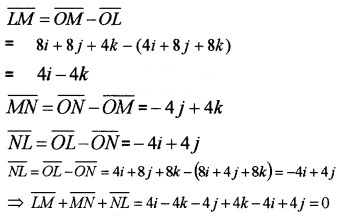
Question 3.
Using the figure answer the following questions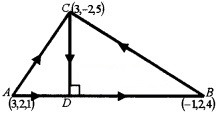

1. Evaluate \(\overline{A B}\).\(\overline{A C}\) (2)
2. Find \(\overline{A D}\) . (2)
3. Find the coordinates of D.

Answer:
1. \(\overline{A B}\) = p.v of B – p.v of A= -4i + 0j + 3k
\(\overline{A C}\) = p.v of C – p.v of A = 0i – 4 j + 4k
\(\overline{A B}\).\(\overline{A C}\) = -4 × 0 + 0 × -4 + 3 × 4 = 12

2.

3. Let the coordinate of D be (x, y ,z)
⇒ \(\overline{A D}\) = (x – 3)i + (y – 2)j + (z – 1)k,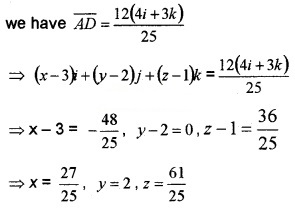

Question 4.
Consider the Parallelogram ABCD

1. Find \(\overline{A B}\) and \(\overline{A D}\) (1)
2. Find the area of the parallelogram ABCD. (1)
3. Find \(\overline{A C}\). (2)
4. Find co-ordinate of C. (2)

Answer:
1. \(\overline{A B}\) = p.v of B – p. v of A
= 3i + 5j + 8k – (i + 2j + k) = 2i + 3j + 7k
\(\overline{A D}\) = p.v of D – p. v of A
= i + 3j + 2k – (i + 2j + k)= 0i + j + k.

2.

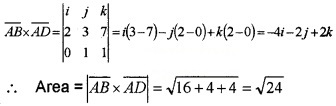
3. By triangle inequality;

4. Let the co-ordinate of C be (x, y, z)
Then, \(\overline{A C}\) = (x – 1)i + (y – 2)j + (z – 1)k = 2i + 4j + 8k
x – 1 = 2 ⇒ x = 3, y – 2 = 4 ⇒ y = 6,
z – 1 = 8 ⇒ z = 9
Co-ordinate of C is (3, 6, 9).

Question 5.
Consider the following quadrilateral ABCD in which P, Q, R, S are the midpoints of the sides.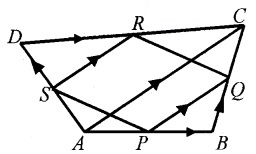

1. Find \(\overline{P Q}\) and \(\overline{S R}\) in terms of \(\overline{A C}\) (2)
2. Show that PQRS is a parallelogram. (2)
3. If \(\bar{a}\) is any vector, prove that (2)

Answer:
1. Using triangle law of addition, we get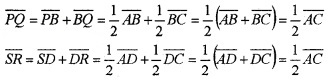

2. From the above explanation we have,

and parallel. Similarly, |\(\overline{S P}\)| = |\(\overline{R Q}\)|
Therefore, PQRS is a parallelogram.

3. Let \(\bar{a}\) = a₁ i + a₂ j + a₃ k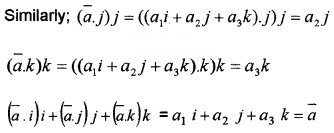

Plus Two Mathematics All Chapters Question and Answers

• Plus Two Mathematics Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 1 Relations and Functions Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 2 Inverse Trigonometric Functions Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 3 Matrices Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 4 Determinants Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 5 Continuity and Differentiability Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 6 Application of Derivatives Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 7 Integrals Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 8 Application of Integrals Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 9 Differential Equations Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 10 Vector Algebra Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 11 Three Dimensional Geometry Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 12 Linear Programming Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 13 Probability Chapter Wise Question and Answers PDF

Benefits of the Plus Two Maths Chapter 10 Vector Algebra Chapter Wise Question and Answers PDF

The Plus Two Maths Chapter 10 Vector Algebra Chapter Wise Question and Answers PDF that has been provided above is extremely helpful for all students because of the way it has been drafted. It is designed by teachers who have over 10 years of experience in the field of education. These teachers use the help of all the past years’ question papers to create the perfect Plus Two Maths Chapter 10 Vector Algebra Chapter Wise Question and Answers PDF.

FAQ’s Plus Two Maths Chapter 10 Vector Algebra Chapter Wise Question and Answers PDF

Where can I download Plus Two Maths Chapter 10 Vector Algebra Chapter Wise Question and Answers PDF?

You can download Plus Two Maths Chapter 10 Vector Algebra Chapter Wise Question and Answers PDF for the latest 2021 session.

Can I download Plus Two All subjects Question and Answers PDF?

Yes - You can click on the links above and download subject wise question papers in PDF

Is there any charge for the Plus Two Maths Chapter 10 Vector Algebra Chapter Wise Question and Answers PDF?

There is no charge for the model papers for you can download everything free