Plus Two Maths Chapter 9 Differential Equations Chapter Wise Question and Answers PDF Download

Plus Two Maths Chapter 9 Differential Equations Chapter Wise Question and Answers PDF Download: Students of Standard 12 can now download Plus Two Maths Chapter 9 Differential Equations chapter wise question and answers pdf from the links provided below in this article. Plus Two Maths Chapter 9 Differential Equations Question and Answer pdf will help the students prepare thoroughly for the upcoming Plus Two Maths Chapter 9 Differential Equations exams.

Plus Two Maths Chapter 9 Differential Equations Chapter Wise Question and Answers

Plus Two Maths Chapter 9 Differential Equations question and answers consists of questions asked in the previous exams along with the solutions for each question. To help them get a grasp of chapters, frequent practice is vital. Practising these questions and answers regularly will help the reading and writing skills of students. Moreover, they will get an idea on how to answer the questions during examinations. So, let them solve Plus Two Maths Chapter 9 Differential Equations chapter wise questions and answers to help them secure good marks in class tests and exams.

Board	Kerala Board
Study Materials	Chapter wise Question and Answers
For Year	2021
Class	12
Subject	Mathematics
Chapters	Maths Chapter 9 Differential Equations
Format	PDF
Provider	Spandanam Blog

How to check Plus Two Maths Chapter 9 Differential Equations Question and Answers?

1. Visit our website - https://spandanamblog.com
2. Click on the 'Plus Two Question and Answers'.
3. Look for your 'Plus Two Maths Chapter 9 Differential Equations Question and Answers'.
4. Now download or read the 'Class 12 Maths Chapter 9 Differential Equations Question and Answers'.

Plus Two Maths Chapter 9 Differential Equations Question and Answers PDF Download

We have provided below the question and answers of Plus Two Maths Chapter 9 Differential Equations Chapter wise study material which can be downloaded by you for free. These Plus Two Maths Chapter 9 Differential Equations Chapter Wise Question and answers will contain important questions and answers and have been designed based on the latest Plus Two Maths Chapter 9 Differential Equations, books and syllabus. You can click on the links below to download the Plus Two Maths Chapter 9 Differential Equations Chapter Wise Question and Answers PDF. 

Question 1.
y = e^2x(a + bx), a and b are arbitrary constants.
Answer:
y = e^2x(a + bx) ____(1)
Differentiating with respect to x,
\(\frac{d y}{d x}\) = e^2xb + (a + bx)2e^2x
\(\frac{d y}{d x}\) = 2y + be^2x ⇒ \(\frac{d y}{d x}\) – 2y = be^2x ____(2)
Differentiating (2) with respect to x,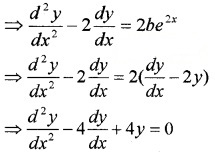

Question 2.
y = e^x(acosx + 6sinx), a and b are arbitrary constants.
Answer:
y = e^x(acosx + 6sinx) ___(1)
Differentiating with respect to x,
\(\frac{d y}{d x}\) = e^x(-asinx + bcosx) + e^x(acosx + bsinx) \(\frac{d y}{d x}\) = e^x(-asin x + b cos x) + y
\(\frac{d y}{d x}\) – y = e^x(-a sin x + b cos x) ____(2)
Differentiating (2) with respec to x,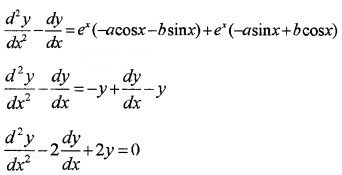

Question 3.
y = c₁e^x + c₂ e^-x , c₁ and c₁ are arbitrary constants.
Answer:
y = c₁e^x + c₂ e^-x ___(1)
Differentiating with respect to x,
\(\frac{d y}{d x}\) = c₁e^x + c₂ e^-x __(2)
Differentiating (2) with respect to x,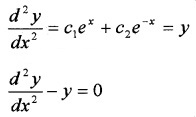

Question 4.
(x – a)² + 2y² = a², a is a arbitrary constants.
Answer:
(x – a)² + 2y² = a² ___(1)
Differentiating with respect to x,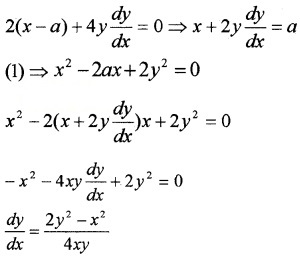

Question 5.
Find the equation of a curve passing through the point (0, -2) given that at any point (x, y) on the curve, the product of the slope of its tangent and y coordinate of the point is equal to the x coordinate of the point.
Answer:
y\(\frac{d y}{d x}\) = x ⇒ ydy = xdx
Integrating on both sides,
∫ydy = ∫xdx + c
⇒ \(\frac{y^{2}}{2}=\frac{x^{2}}{2}\) + c ____(1)
Since it passes through (0, -2),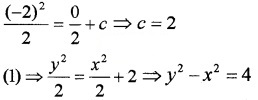

Question 6.
Form the DE representing the family of parabolas having a vertex at origin and axis along positive direction of x-axis.
Answer:
Let (a, 0) be focus of the given family of parabolas.
y² = 4ax ____(1)
Differentiating with respect to x,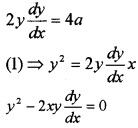

Question 7.
For the DE xy \(\frac{d y}{d x}\) = (x + 2)(y + 2), find the solution curve passing through the point(1,- 1).
Answer:
xy \(\frac{d y}{d x}\) = (x + 2)(y + 2)
⇒ \(\frac{y}{y+2} d x=\frac{x+2}{x} d x\)
Integrating on both sides,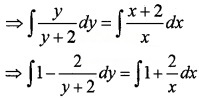

⇒ y – 2 log|y + 2| = x + 2log|x| + c ____(1)
Since it passes through (1, -1),
⇒ -1 – 2log|-1 + 2| = 1 + 2log|l| + c
⇒ -2 = c
(1) ⇒ y – 2log|y + 2| = x + 2log|x| – 2.

Question 8.
Solve the initial value problem: \(\frac{d y}{d x}\) = y tan 2x; y(0) = 2.
Answer:
\(\frac{d y}{d x}\) = y tan 2x
⇒ \(\frac{d y}{y}\) tan 2xdx,
This is a variable type
∴∫\(\frac{d y}{y}\) = ∫tan 2xdx ⇒ log y = \(\frac{1}{2}\) log|sec 2x| + c
Given y(0) = 2 ⇒ log 2 = \(\frac{1}{2}\) log|sec 0| + c ⇒ c = log 2
log y = \(\frac{1}{2}\) log|sec 2x| + log 2 ⇒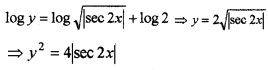

Plus Two Maths Differential Equations Four Mark Questions and Answers

Question 1.
(i) Consider the differential equation given below. (1)
\(\frac{d^{4} y}{d x^{4}}-\sin \left(\frac{d^{3} y}{d x^{3}}\right)=0\). Write the order and degree of the DE (if defined)
(ii) Find the Differential equation satisfying the family of curves y² = a(b² – x²), a and b are arbitrary constants. (3)
Answer:
(i) 4; degree is not defined

(ii) y² = a(b² – x²) ____(1)
Differentiating with respect to x,
2y \(\frac{d y}{d x}\) = -a2x ⇒ y\(\frac{d y}{d x}\) = -ax ____(2)
Differentiating (2) with respect to x,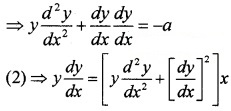

Which is the differential equation.

Question 2.

1. Find the Differential equation satisfying the family of curves y = ae^3x + be^-2x, a and b are arbitrary constants. (3)
2. Hence write the degree and order of the DE. (1)

Answer:
1. y = ae^3x + be^-2x ____(1)
Differentiating with respect to x,
\(\frac{d y}{d x}\) = ae^3x × 3 + be^-2x × -2 ____(2)
Differentiating (2) with respect to x,
⇒ \(\frac{d^{2} y}{d x^{2}}\) = 9ae^3x + 4be^-2x ____(3)
Now, (3) + 2 × (2) ⇒ \(\frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}=15 a e^{3 x}\)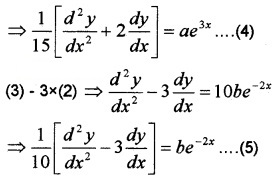

Using (4), (5) in (1), we have,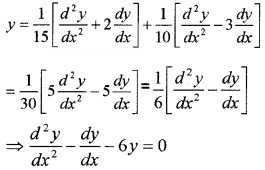

2. Order: 2; degree: 1.

Question 3.
Consider the equation of all circles which pass through the origin and whose centres are on the x-axis.

1. Define the general equation of the circle.(1)
2. Find the DE corresponding to the above equation. (3)

Answer:
1. The general equation of the circle, passing through the origin and whose centers lies on x-axis can be taken as (x – h)² + y² = h² where h being an arbitrary constant.

2. Simplifying (x – h)² + y² = h² we get,
x² – 2hx + h² + y² = h² ⇒ x² – 2hx + h² = 0 _____(1)
Differentiating we get,
2x + 2y \(\frac{d y}{d x}\) – 2h = 0 ⇒ h = x + y \(\frac{d y}{d x}\)
Substituting in (1) we can eliminate h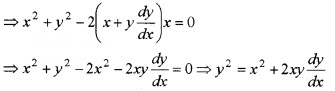

Question 4.
Find a particular solution satisfying the given condition. (x³ + x² + x +1)\(\frac{d y}{d x}\) = 2x² + x, y = 1, when x = 0.
Answer: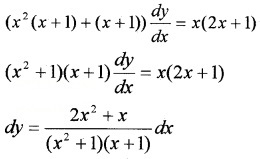

Integrating on both sides,
∫dy = ∫\(\frac{2 x^{2}+x}{\left(x^{2}+1\right)(x+1)} d x\)
Splitting into partial fractions we have, (see Unit:7)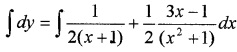

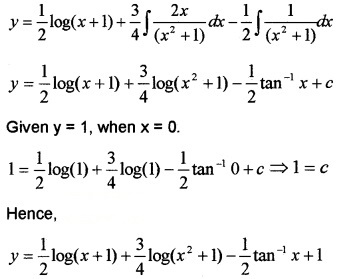
Question 5.

1. Write the degree of the DE y’ = 2xy. [0, 1, 2, 3] (1)
2. Express y’ = 2xy in the form Mdx = Ndy. Where M is a function of x and N is the function of y. (2)
3. Solve y’ = 2xy, y(0) = 1 (1)

Answer:

1. Degree = 1

2. We have, \(\frac{d y}{d x}\) = 2xy ⇒ \(\frac{d y}{y}\) = 2xdx, which is of the form Mdx = Ndy.

3. Solution is ∫\(\frac{d y}{y}\) = 2∫xdx ⇒ log|y| = x² + c
Given y(0) = 1 ⇒ log|1| = 0 + c ⇒ c = 0
⇒ log|y| = x² ⇒ y = e^x2.

Question 6.
Solve the following DE \(\frac{d y}{d x}=\frac{y^{2}-x^{2}}{2 x y}\).
Answer:
\(\frac{d y}{d x}=\frac{y^{2}-x^{2}}{2 x y}\), this is a Homogeneous DE.
Therefore, put y = vx and \(\frac{d y}{d x}\) = v + x\(\frac{d v}{d x}\) to convert it into variable separable form.
The DE becomes,

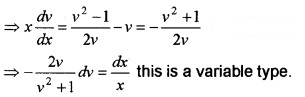
Therefore integrating we get,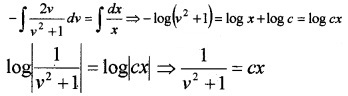

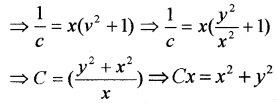
Question 7.
Solve the linear differential equation \(x \frac{d y}{d x}-y=(x-1) e^{x}\).
Answer:
Given, x\(\frac{d y}{d x}\) – y = (x – 1)e^x, dividing both sides by x ,we get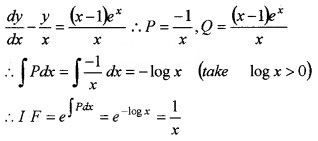

Solution is
y × IF = ∫Q(IF)dx + c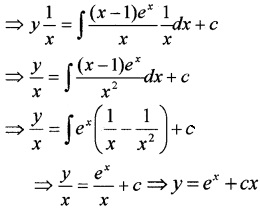

Question 8.
(i) Choose the correct answer from the bracket. The solution of the differential equation xdy + ydx = 0 represents (1)
(a) a rectangular hyperbola
(b) a parabola whose centre is origin
(c) a straight line whose centre is origin
(d) a circle whose centre is origin.
(ii) From the DE of the family of circles touching the x-axis at origin. (3)
Answer:
(i) (c) a straight line whose centre is origin.

(ii) Let (0, a) be the centre of the circle. Therefore the equation of the circle is
x² + (y – a)² = a²
⇒ x² + y² = 2ay
⇒ \(\frac{x^{2}+y^{2}}{y}\) = 2a ____(1)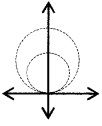

Differentiating with respect to x,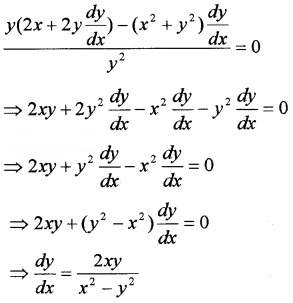

Question 9.
Solve the DE x²\(\frac{d y}{d x}\) = x² – 2y² + xy.
Answer:
x²\(\frac{d y}{d x}\) = x² – 2y² + xy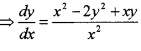

this is a Homogeneous DE.
Put y = vx and \(\frac{d y}{d x}=v+x \frac{d v}{d x}\)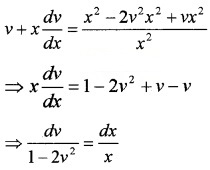

Integrating on both sides,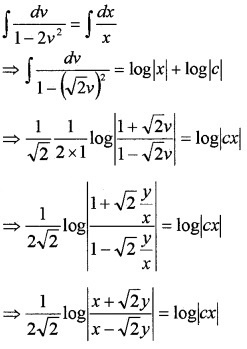

Question 10.
Choose the correct answer from the bracket

1. The DE \(\frac{d y}{d x}+\frac{y}{x}\) = e^x, x > 0 is of order …..[0,1,2,3] (1)
2. The integrating factor \(\frac{d y}{d x}+\frac{y}{x}\) = e^x, is……..[x, e^x, -x, e^-x] (1)
3. Solve \(\frac{d y}{d x}+\frac{y}{x}\) = e^x (2)

Answer:
1. Order = 1

2. \(\frac{d y}{d x}+\frac{y}{x}\) = e^x is of the form \(\frac{d y}{d x}\) + Py = Q,
where P = \(\frac{1}{x}\), Q = e^x
IF = e^∫Pdx = e^{∫\(\frac{1}{x}\)dx} = e^logx = x

3. Solution is y.IF = ∫e^x. IFdx
⇒ yx = ∫x.e^xdx ⇒ yx = x.e^x – ∫e^xdx
⇒ yx = x.e^x – e^x + c ⇒ yx = e^x(x – 1) + c.

Question 11.
Solve the DE \(\frac{d y}{d x}=\frac{x+y}{x-y}\).
Answer:
\(\frac{d y}{d x}=\frac{x+y}{x-y}\), this is a Homogeneous DE.
Put y = vx and \(\frac{d y}{d x}\) = v + x\(\frac{d v}{d x}\)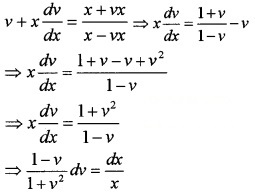

Integrating on both sides,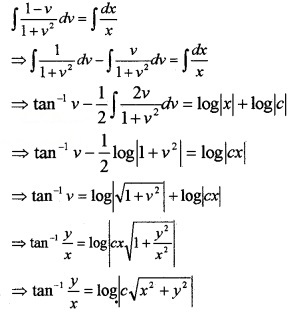

Plus Two Maths Differential Equations Six Mark Questions and Answers

Question 1.
Consider the DE \(\frac{d y}{d x}=\frac{y^{3}+3 x^{2} y}{x^{3}+3 x y^{2}}\)

1. Identify the DE ? Give reason. (1)
2. Explain the method of solving the DE. (1)
3. Solve the DE. (4)

Answer:
1. Given DE is a Homogeneous DE. Since y³ + 3x²y and x³ + 3xy² are Homogeneous functions of same degree (deg = 3).

2. By giving a substitution y = v x and \(\frac{d y}{d x}\) = v + x\(\frac{d y}{d x}\)
we can convert the DE into variable separable.

3. Now we have, \(\frac{d y}{d x}=\frac{y^{3}+3 x^{2} y}{x^{3}+3 x y^{2}}\)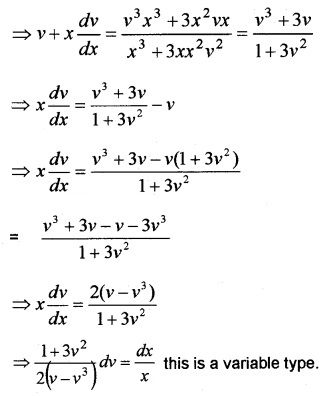

∴ Integrating we get,
\(\int \frac{1+3 v^{2}}{2 v\left(1-v^{2}\right)} d v=\int \frac{d x}{x}\)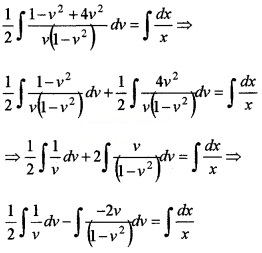

\(\frac{1}{2}\) log v – log(1 – v²) = log x + log c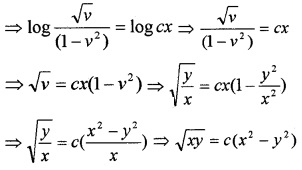

Question 2.
Consider the D.E \(\frac{d y}{d x}+\frac{y}{x}=x^{2}\)

1. Find degree and order of DE . (1)
2. Solve the D.E. (4)
3. Find the particular solution when x = 1, y = 1. (1)

Answer:
1. Degree: 1, Order: 1.

2. The given D.E is first order linear DE of the form
\(\frac{d y}{d x}\) + Py = Q. Comparing we get, P = \(\frac{1}{x}\), Q = x²
∴ ∫Pdx = ∫\(\frac{1}{x}\)dx = logx
Integrating factor (I.F) = e^∫Pdx = e^logx = x
y.x = ∫x².xdx + c = ∫x³ dx + c
⇒ y.x = \(\frac{x^{4}}{4}\) + c ___(1)

3. Given, y = 1 when x = 1, then (1)
⇒ 1 × 1 = \(\frac{1}{4}\) + c ⇒ c = \(\frac{3}{4}\)
Therefore particular solution is
y.x = \(\frac{x^{4}}{4}\) + \(\frac{3}{4}\) ⇒ 4xy = x³ + 3.

Question 3.
Consider the equation.\(\frac{d y}{d x}\) + y = sin x

1. What is the order and degree of this equation? (1)
2. Find the integrating factor. (2)
3. Solve this equation. (3)

Answer:
1. Order = 1, Degree = 1

2. Given, \(\frac{d y}{d x}\) + y = sin x is of the form
\(\frac{d y}{d x}\) + Py = Q ⇒ P = 1, Q = sinx
Integrating factor = e^∫Pdx = e^∫1dx = e^x

3. Therefore solution is
y.IF = ∫Q.IFdx + c ⇒ ye^x = ∫e^x sinxdx + c ____(1)
∫sinx.e^xdx = e^x sinx – ∫cosx.e^xdx
= e^x sin x – cosx.e^x – ∫sinx.e^x dx
⇒ 2∫e^x sin xdx = e^x(sin x – cos x)
⇒ ∫e^x sinxdx = \(\frac{e^{x}}{2}\)(sinx – cosx)
(1) ⇒ ye^x = \(\frac{e^{x}}{2}\)(sinx – cosx) + c.

Question 4.
Considerthe D.E (x² – 1)\(\frac{d y}{d x}\) + 2(x + 2)y = 2(x + 1)

1. Find \(\frac{d y}{d x}\), degree and order of the above differential equation. (1)
2. Find the integrating factor of the above differential equation. (2)
3. Solve the differential equation. (3)

Answer:
1. Given, (x² – 1)\(\frac{d y}{d x}\) + 2(x + 2)y = 2(x + 1)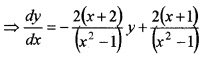

Here, Degree = 1, Order = 1.

2. The given DE is of the form \(\frac{d y}{d x}\) + Py = Q
Where,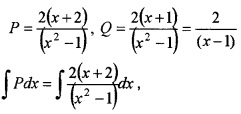

Splitting it into partial fractions we get,

Put x = 1, ⇒ 6 = 2B ⇒ B = 3,
put x = -1, ⇒ 2 = -2A ⇒ A = -1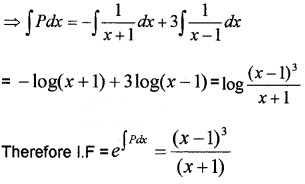

3. Solution is y × IF = ∫Q × IFdx + c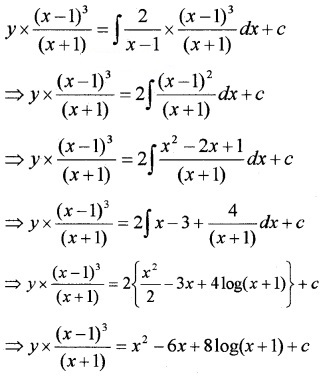

Question 5.
(i) The degree of the differential Equation \(\frac{d^{2} y}{d x^{2}}+\cos \left(\frac{d y}{d x}\right)=0\) is
(a) 2
(b) 1
(c) 0
(d) Not defined
(ii) Solve \(\frac{d y}{d x}\) + 2y tanx = sinx; y = 0, x = \(\frac{\pi}{3}\) (5)
Answer:
(i) (d) Not defined.

(ii) \(\frac{d y}{d x}\) + 2y tanx = sinx
Then, P = 2tanx, Q = sinx
IF = e^∫Pdx = e^∫2tanxdx = e^{2log sec x} = sec² x Solution is; y × IF = ∫Q(IF)dx + c
⇒ ysec² x = ∫sinx sec² xdx + c
⇒ ysec² x = ∫tanx secx dx + c
⇒ ysec²x = secx + c
Here; y = 0, x = \(\frac{\pi}{3}\)
⇒ 0 × sec² \(\frac{\pi}{3}\) = sec\(\frac{\pi}{3}\) + c ⇒ c = -2
⇒ ysec² x = secx – 2.

Question 6.
(i) The order of the differential equation \(x^{4} \frac{d^{2} y}{d x^{2}}=1+\left(\frac{d y}{d x}\right)^{3}\) is
(a) 1
(b) 3
(c) 4
(d) 2
(ii) Find the particular solution of the (1 + x²) \(\frac{d y}{d x}\) + 2 xy = \(\frac{1}{1+x^{2}}\); y = 0, when x = 1 (5)
Answer:
(i) (d) 2

(ii) (1 + x²) \(\frac{d y}{d x}\) + 2 xy = \(\frac{1}{1+x^{2}}\); y = 0, when x = 1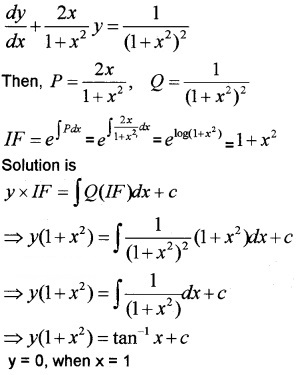

⇒ 0(1 + 1²) = tan^-11 + c ⇒ c = \(-\frac{\pi}{4}\)
⇒ y(1 + x²) = an^-1x – \(\frac{\pi}{4}\).

Plus Two Mathematics All Chapters Question and Answers

• Plus Two Mathematics Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 1 Relations and Functions Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 2 Inverse Trigonometric Functions Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 3 Matrices Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 4 Determinants Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 5 Continuity and Differentiability Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 6 Application of Derivatives Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 7 Integrals Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 8 Application of Integrals Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 9 Differential Equations Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 10 Vector Algebra Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 11 Three Dimensional Geometry Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 12 Linear Programming Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 13 Probability Chapter Wise Question and Answers PDF

Benefits of the Plus Two Maths Chapter 9 Differential Equations Chapter Wise Question and Answers PDF

The Plus Two Maths Chapter 9 Differential Equations Chapter Wise Question and Answers PDF that has been provided above is extremely helpful for all students because of the way it has been drafted. It is designed by teachers who have over 10 years of experience in the field of education. These teachers use the help of all the past years’ question papers to create the perfect Plus Two Maths Chapter 9 Differential Equations Chapter Wise Question and Answers PDF.

FAQ’s Plus Two Maths Chapter 9 Differential Equations Chapter Wise Question and Answers PDF

Where can I download Plus Two Maths Chapter 9 Differential Equations Chapter Wise Question and Answers PDF?

You can download Plus Two Maths Chapter 9 Differential Equations Chapter Wise Question and Answers PDF for the latest 2021 session.

Can I download Plus Two All subjects Question and Answers PDF?

Yes - You can click on the links above and download subject wise question papers in PDF

Is there any charge for the Plus Two Maths Chapter 9 Differential Equations Chapter Wise Question and Answers PDF?

There is no charge for the model papers for you can download everything free