Plus Two Maths Chapter 5 Continuity and Differentiability Chapter Wise Question and Answers PDF Download

Plus Two Maths Chapter 5 Continuity and Differentiability Chapter Wise Question and Answers PDF Download: Students of Standard 12 can now download Plus Two Maths Chapter 5 Continuity and Differentiability chapter wise question and answers pdf from the links provided below in this article. Plus Two Maths Chapter 5 Continuity and Differentiability Question and Answer pdf will help the students prepare thoroughly for the upcoming Plus Two Maths Chapter 5 Continuity and Differentiability exams.

Plus Two Maths Chapter 5 Continuity and Differentiability Chapter Wise Question and Answers

Plus Two Maths Chapter 5 Continuity and Differentiability question and answers consists of questions asked in the previous exams along with the solutions for each question. To help them get a grasp of chapters, frequent practice is vital. Practising these questions and answers regularly will help the reading and writing skills of students. Moreover, they will get an idea on how to answer the questions during examinations. So, let them solve Plus Two Maths Chapter 5 Continuity and Differentiability chapter wise questions and answers to help them secure good marks in class tests and exams.

Board	Kerala Board
Study Materials	Chapter wise Question and Answers
For Year	2021
Class	12
Subject	Mathematics
Chapters	Maths Chapter 5 Continuity and Differentiability
Format	PDF
Provider	Spandanam Blog

How to check Plus Two Maths Chapter 5 Continuity and Differentiability Question and Answers?

1. Visit our website - https://spandanamblog.com
2. Click on the 'Plus Two Question and Answers'.
3. Look for your 'Plus Two Maths Chapter 5 Continuity and Differentiability Question and Answers'.
4. Now download or read the 'Class 12 Maths Chapter 5 Continuity and Differentiability Question and Answers'.

Plus Two Maths Chapter 5 Continuity and Differentiability Question and Answers PDF Download

We have provided below the question and answers of Plus Two Maths Chapter 5 Continuity and Differentiability Chapter wise study material which can be downloaded by you for free. These Plus Two Maths Chapter 5 Continuity and Differentiability Chapter Wise Question and answers will contain important questions and answers and have been designed based on the latest Plus Two Maths Chapter 5 Continuity and Differentiability, books and syllabus. You can click on the links below to download the Plus Two Maths Chapter 5 Continuity and Differentiability Chapter Wise Question and Answers PDF. 

Question 1.
Consider the function g(x) = \(\frac{|x-2|}{x-2}\)

1. Find the domain and range of the function g(x). (2)
2. Check whether the g(x) is continuous at x = 2. (1)

Answer:
1. The function is not defined at points where the denominator is zero.
i.e., x – 2 = 0 ⇒ x = 2.
∴ domain is R – {2}.
g(x) = \(\frac{|x-2|}{x-2}\) = \(\left\{\begin{array}{c}{\frac{x-2}{x-2}, \quad x-2>0} \\{\frac{-(x-2)}{x-2}, \quad x-2<0}\end{array}=\left\{\begin{array}{ll}{1,} & {x>2} \\{-1,} & {x<2}\end{array}\right.\right.\)
∴ range is {-1, 1}

2. The function g(x) is not defined at x = 2. Therefore discontinuous.

Question 2.
(i) If f(x) = x+|x| + 1, then which of the follow represents f (x) (1)


(ii) Test whether f (x) is continuous at x=0. Explain. (2)
Answer:
(i) (b) Since, f(x) = \(\left\{\begin{array}{c}{x+x+1, x \geq 0} \\{x-x+1, \quad x<0}
\end{array}=\left\{\begin{array}{c}{2 x+1, x \geq 0} \\{1, x<0}\end{array}\right.\right.\)

(ii) We have ,f (0) = 1,

Continuous at x = 0.

Question 3.
Consider the function f(x) = \(\left\{\begin{array}{ll}{\frac{\sin x}{x}} & {, x<0} \\{x+1} & {, x \geq 0}\end{array}\right.\)

1. Find \(\lim _{x \rightarrow 0} f(x)\) (2)
2. Is f (x) continuous at x= 0? (1)

Answer:
1. To find \(\lim _{x \rightarrow 0} f(x)\) we have to find f(0^– )and f(0⁺)
f(0^–) = \(\lim _{x \rightarrow 0} \frac{\sin x}{x}=1\),
f(0⁺) = \(\lim _{x \rightarrow 0}\) + 1 = 0 + 1 = 1
f(0^–) = f(0⁺) = 1 .Therefore \(\lim _{x \rightarrow 0} f(x)\) = 1

2. Here, f (0) = 0 + 1 = 1 = f(0^–) = f(0⁺) = 1
Therefore continuous at x = 0.

Question 4.
Consider the figure and answer the following questions.

(i) Identify the graphed function. (1)

(ii) Discuss the continuity of the above function at x = 2. (2)
Answer:
(i) (b) f(x) = \(\left\{\begin{array}{ll}{\frac{|x-2|}{x-2},} & {x \neq 2} \\{0,} & {x=2}\end{array}\right.\)

(ii) From the figure we can see that
f(2^–) = 1, f(2⁺) = -1 and f(2) = 0
Therefore, f(2^–) = 1 ≠ f(2⁺) = -1 ≠ f(2) = 0. Discontinuous.

Question 5.
Consider f(x) = \(\left\{\begin{array}{ll}{2 x} & {\text { if } x<2} \\{2} & {\text { if } x=2} \\ {x^{2}} & {\text { if } x>2}\end{array}\right.\)
(a) Find \(\lim _{x \rightarrow 2^{-}} f(x)\) and \(\lim _{x \rightarrow 2^{+}} f(x)\) (2)
(b) f(x) is continuous. If not so, how can you make it continuous. (1)
Answer:

Therefore f(x) is not continuous at x = 2.
If f(2) = 4, then f(x) becomes continuous.

Question 6.
If y = log₁₀x + log_x10 + log_xx + log₁₀10. Find \(.
Answer:
y = log_e x log₁₀e + log_e10 log_xe + 1 + 1

Question 7.
Examine the continuity of the function

Answer:
In both the intervals x = 1 and x < 1 the function f(x) is a polynomial so continuous. So we have to check the continuity at x = 1.

f(1) = 2
Since

f(x) is continuous at x = 1.

Question 8.
Find [latex]\frac{d y}{d x}\) of the following (3 score each)

1. 2x + 3y = sinx
2. xy + y² = tanx + y
3. x³ + x²y + xy² + y³ = 81
4. sin²x + cos²y = 1
5. \(\sqrt{x}\) + \(\sqrt{y}\) = 1
6. x² + xy + y² = 7
7. x²(x – y) = y²(x + y)
8. xy² + x²y = 2
9. sin y = xcos (a + y)

Answer:
1. Given; 2x + 3y = sinx
Differentiating with respect to x;

2. Given; xy + y² = tanx + y
Differentiating with respect to x;

3. Given; x³ + x²y + xy² + y³ = 81
Differentiating with respect to x;

4. Given; sin²x + cos²y = 1
Differentiating with respect to x;

5. \(\sqrt{x}\) + \(\sqrt{y}\) = 1
Differentiating with respect to x;

6. x² + xy + y² = 7
Differentiating with respect to x;

7. x²(x – y) = y²(x + y)
Differentiating with respect to x;

8. xy² + x²y = 2
Differentiating with respect to x;

9. sin y = xcos (a + y)
⇒ x = \(\frac{\sin y}{\cos (a+y)}\)
Diff. with respect to y.

Question 9.
Find \(\frac{d y}{d x}\) of the following (3 score each)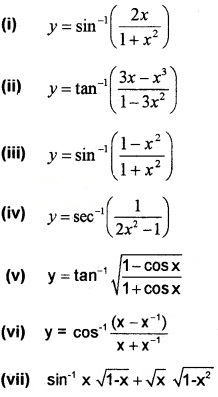

(viii) x = a(t – sint), y = a(1 – cost)
(ix) y = e^t cost, x = e^t sint.
Answer:
(i) We know; y = sin^-1\(\left(\frac{2 x}{1+x^{2}}\right)\)
⇒ y = = 2 tan^-1(x)
Differentiating with respect to x;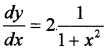

(ii) We know; y = tan^-1\(\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right)\)
Put x = tanθ ⇒ θ = tan^-1x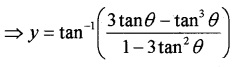

⇒ y = tan^-1(tan3θ)
⇒ y = 3 tan^-1(x)
Differentiating with respect to x;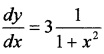

(iii) We know; y = sin^-1\(\left(\frac{1-x^{2}}{1+x^{2}}\right)\)
Put x = tanθ ⇒ θ = tan^-1x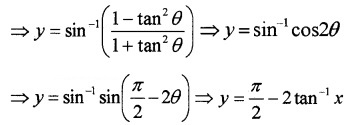

(iv) We know; y = sec^-1 = \(\left(\frac{1}{2 x^{2}-1}\right)\)
Put x = cosθ ⇒ θ = cos^-1x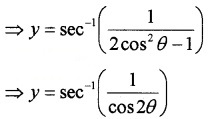

⇒ y = sec^-1 sec2θ = 2θ
⇒ y = 2cos^-1(x)
Differentiating with respect to x;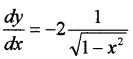

(v) ∴ y = tan^-1\(\sqrt{\tan ^{2} x / 2}\) = tan^-1 tanx/2 = x/2
\(\frac{d y}{d x}=\frac{1}{2}\).

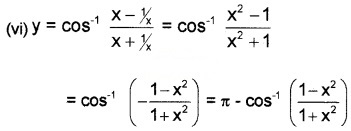
= π – 2tan^-1x
\(\frac{d y}{d x}=\frac{-2}{1+x^{2}}\).

(vii) Let x = sinθ and \(\sqrt{x}\) = sinφ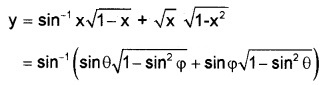

= sin^-1 (sinθcosφ + cosφsinφ)
= sin^-1 (sin(θ + φ)) = θ + φ
= sin^-1x + sin^-1\(\sqrt{x}\)
\(\frac{d y}{d x}=\frac{1}{\sqrt{1-x^{2}}}+\frac{1}{\sqrt{1-x}} \times \frac{1}{2 \sqrt{x}}\).

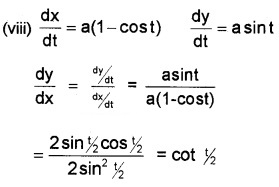
(ix) y = e^tcost ⇒ \(\frac{d y}{d t}\) = – e^t sin t + e^t
x = e^t sint ⇒ \(\frac{d x}{d t}\) = e^t cos t + e^t sin t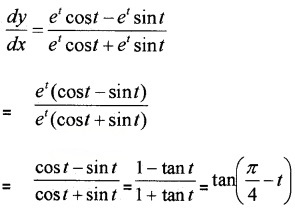

Question 10.
If y = log\(\left(\frac{1}{x}\right)\), Show that \(\frac{d y}{d x}\) + e^y = 0.
Answer:
Given, y = log\(\left(\frac{1}{x}\right)\) ? \(\left(\frac{1}{x}\right)\) = e^y …….(1)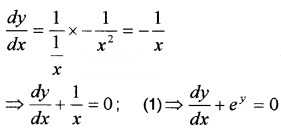

Question 11.
If e^y (x+1) = 1. Show that

1. \(\frac{d y}{d x}\) = -e^y (2)
2. \(\frac{d^{2} y}{d x^{2}}=\left(\frac{d y}{d x}\right)^{2}\) (1)

Answer:
1. e^y (x+1) = 1
Differentiating e^y +e^y(x +1) \(\frac{d y}{d x}\) = 0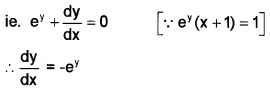

2.

Question 12.
(i) Evaluate \(\lim _{x \rightarrow 0} \frac{k \cos x}{\pi-2 x}\) (2)
(Hint: Put π – 2x = y , where Iris a constant)
(ii) Find the value of k if f (x) is a continuous function given by (1)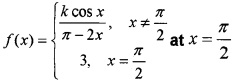

Answer:
(i) \(\lim _{x \rightarrow \pi / 2} \frac{k \cos x}{\pi-2 x}=k \lim _{x \rightarrow \pi / 2} \frac{\cos x}{\pi-2 x}\),
Put π – 2x = y when Put x → π/2, y → 0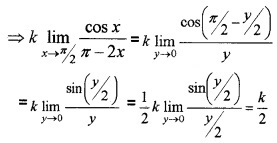

(ii) Since f (x) is continuous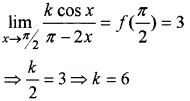

Question 13.
If f(x) \(f(x)=\left\{\begin{array}{cc}{x-[x]} & {, x<.2} \\{0} & {; x=2} \\{3 x-5} & {, x>2}
\end{array}\right.\)

1. Find \(\lim _{x \rightarrow 2} f(x)\) (2)
2. Is f(x) continuous at x = 2? (1)

Answer:
1. To find \(\lim _{x \rightarrow 2} f(x)\)
we have to find f(2^–) and f(2⁺)
f(2^–) = \(\lim _{x \rightarrow 2} x-[x]\) = 2 -1 = 1,
f(2⁺) = \(\lim _{x \rightarrow 2}\) 3x – 5 = 6 -5 = 1
f(2^–) = f(2⁺) = 1.
Therefore \(\lim _{x \rightarrow 2}\) f(x) = 1

2. Here, f(2) = 0 ≠ f(2^–) = f(2⁺) = 1.
Therefore discontinuity at x = 2.

Plus Two Maths Continuity and Differentiability Four Mark Questions and Answers

Question 1.
If x = 2cosθ; y = 3sinθ

1. Find \(\frac{d y}{d x}\).
2. Find \(\frac{d^{2} y}{d x^{2}}\)

Answer:
1. x = 2cosθ ⇒ \(\frac{d x}{d θ}\) = -2sinθ
y = 3sinθ ⇒ \(\frac{d x}{d θ}\) = 3cosθ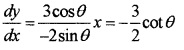

2.

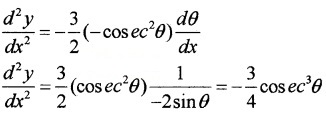
Question 2.
If y = (tan^-1 x)², show that (x² +1)² y₂ + 2x(x² +1) y₁ = 2.
Answer:
y = (tan^-1 x)²
⇒ y₁ = 2(tan^-1 x) \(\frac{1}{1+x^{2}}\)
⇒ (1 + x²)y₁ = 2(tan^-1 x)
⇒ (1 + x²)y₂ + y₁2x = 2 \(\frac{1}{1+x^{2}}\)
⇒ (1 + x²)² y₂ + x(1 + x²)y₁ = 2.

Question 3.
Find \(\frac{d y}{d x}\) if y = sin^-1 \(\left(\frac{1-x^{2}}{1+x^{2}}\right)\), 0 < x < 1.
Answer:
Put x = tanθ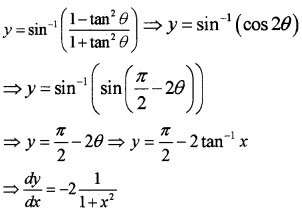

Question 4.
Let f(x) = \(\left\{\begin{array}{ll}{\cos x,} & {0 \leq x \leq c} \\{\sin x,} & {c<x \leq \pi}\end{array}\right.\)

1. Find the value of c if / is continuous on [0, π].
2. Show that is f not differentiable at the point c.

Answer:
1. Since f is continuous on [0, π], we have;
\(\lim _{x \rightarrow c^{+}}\) f(x) = \(\lim _{x \rightarrow c^{-}}\) f(x) = f(c)
⇒ \(\lim _{x \rightarrow c^{+}}\) sinx = \(\lim _{x \rightarrow c^{-}}\) cosx = cosc
⇒ sinc = cosc ⇒ c = \(\frac{π}{4}\).

2. \(f^{\prime}(x)=\left\{\begin{array}{ll}{-\sin x,} & {0 \leq x \leq c} \\{\cos x,} & {c<x \leq \pi}\end{array}\right. \)
Left derivative at \(\frac{\pi}{4}\) = – sin \(\frac{\pi}{4}\) = –\(\frac{1}{\sqrt{2}}\)
Right derivative at \(\frac{\pi}{4}\) = cos \(\frac{\pi}{4}\) = \(\frac{1}{\sqrt{2}}\)
Left derivative at \(\frac{\pi}{4}\) ≠ Right derivative at \(\frac{\pi}{4}\)
Therefore is not differentiable at the point c.

Question 5.

1. Find \(\frac{d y}{d x}\) if x = 2sinθ; y = 3cosθ
2. Which among the following functions is differentiable on R?

(a) |sinx|
(b) |cosx|
(c) cos|x|
(d) sin|x|
Answer:
1. \(\frac{d x}{d θ}\) = 2cosθ; \(\frac{d y}{d θ}\) = -3 sinθ ⇒ \(\frac{d y}{d x}\) = \(-\frac{3}{2}\)tanθ

2. (c) cos|x|
(Since cos x is an even function, it treats x and -x in the same way).

Question 6.
(i) Examine whether the function defined by \(f(x)=\left\{\begin{array}{ll}{x+5,} & {x \leq 1} \\{x-5,} & {x>1}\end{array}\right.\) is continuous or not. (2)
(ii) If x = ^sin-1t, y = ^cos-1t, a > 0, show that \(\frac{d y}{d x}=-\frac{y}{x}\)
Answer: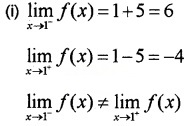

f(x) is not continuous.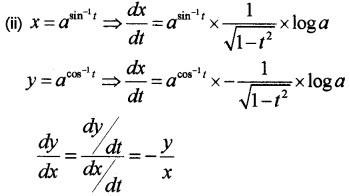

Question 7.
(i) If \(f(x)=\left\{\begin{array}{ll}{1-x,} & {0 \leq x \leq 1} \\{1+x,} & {1<x \leq 2}\end{array}\right.\) then which of the following is not true (1)
(a) f is continuous in ( 0, 1 )
(b) f is continuous in (1, 2 )
(c) f is continuous in [ 0, 2 ]
(d) f is continuous in [ 0,1 ]
if \(\left\{\begin{array}{cc}{1,} & {x \leq 3} \\{a x+b} & {, \quad 3<x<5} \\{7,} & {5 \leq x}\end{array}\right.\)
(ii) Find f(3⁺) and f(5^–) (1)
(iii) Hence find the value of ‘a’ and ‘b’ so that f(x) is continuous. (2)
Answer:
(i) (c) Since f is not continuous at x = 1.

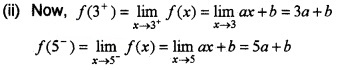
(iii) Since f (x) is continuous, it is continuous at x = 3 and x = 5
∴ f(3⁺) = f(3) ⇒ 3a + b = 1 ____(1)
and f(5^–) = f(5) ⇒ 5a + b = 7 ____(2)
(2) – (1) ⇒ 2a = 6, a = 3
(1) ⇒ b = 1 – 3 a ⇒ b = -8
∴ a = 3, b = – 8.

Question 8.
Consider f(x) = \(\left\{\begin{array}{ll}{2 x+3,} & {x \leq 2} \\{x+2 k,} & {x>2}\end{array}\right.\)

1. Find f(2) (1)
2. Evaluate \(\lim _{x \rightarrow 2^{+}}\)f(x) (1)
3. Find the value of k, if is continuous at x = 2. (2)

Answer:
1. f(2) = 2(2) + 3 = 7

2. Here, f(x) = x + 2k for x > 2.
\(\lim _{x \rightarrow 2^{+}}\)f(x) = \(\lim _{x \rightarrow 2}\)(x + 2k) = 2 + 2k.

3. Since f (x) is continuous at x = 2
We have, f(2) = \(\lim _{x \rightarrow 2^{+}}\)f(x)
⇒ 7 = 2 + 2k ⇒ k = \(\frac{5}{2}\)

Question 9.
Find \(\frac{d y}{d x}\) of the following (4 score each)

1. y = (logx)^cosx
2. x = 2at², y = at⁴
3. x = a(cosθ + θsinθ), y = a(sinθ – θcosθ)
4. y=x^x
5. y =(x log x)^log(logx)
6. y = \(\sqrt{\sin x \sqrt{\sin x+\sqrt{\sin x+\ldots .}}}\)
7. y^x = x^siny
8. y =(log x)^x + x^logx
9. y = (sinx)^x + sin^-1 \(\sqrt{x}\)

Answer:
1. Given; y = (logx)^cosx, taking log on both sides;
log y = cosxlog(logx),
Differentiating with respect to x;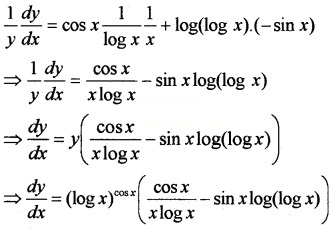

2. Given; x = 2at² ⇒ \(\frac{d x}{d t}\) = 4at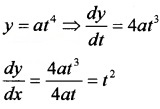

3. Given; x = a(cosθ + θsinθ)
\(\frac{d x}{d \theta}\) = a(-sinθ + θcosθ + sinθ) = aθcosθ
y = a(sinθ – θcosθ)
\(\frac{d x}{d \theta}\) = a(cosθ – θ(-sinθ) – cosθ) = aθ sinθ
\(\frac{d y}{d x}=\frac{a \theta \sin \theta}{a \theta \cos \theta}=\tan \theta\)

4. y= x^x; Taking log on both sides;
log y = x log x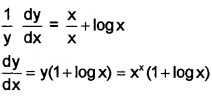

5. y = (x log x)^{log logx}
Taking log on both sides;
log y = (log log x) [log (xlogx)]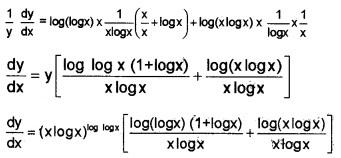

6. y = \(\sqrt{\sin x+y}\) ⇒ y² = sinx + y
⇒ y² – y = sinx

7. y^x = x^{sin y};
Taking log on both sides;
xlogy = siny log x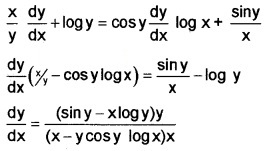

8. y = (log x)^x + x^logx = u + v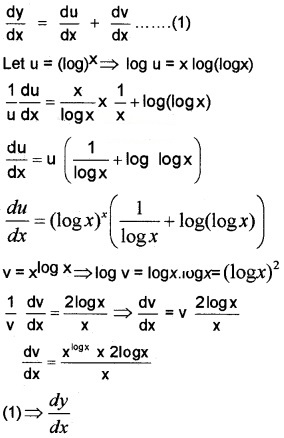

9. y = (sinx)^x + sin^-1\(\sqrt{x}\)
Let u = (sinx)^x ⇒ log u = x log sinx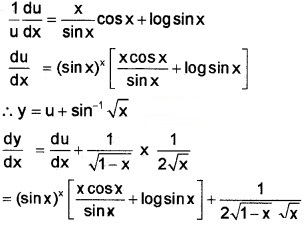

Question 10.
Find \(\frac{d^{2} y}{d x^{2}}\) of the following

1. y = x² + 3x + 2 (2)
2. y = tan^-1x (2)

Answer:
1. Given; y = x² + 3x + 2
Differentiating with respect to x;
\(\frac{d y}{d x}\) = 2x + 3
Differentiating again with respect to x;
\(\frac{d^{2} y}{d x^{2}}\) = 2.

2. Given; y = tan^-1x
Differentiating with respect to x; \(\frac{d y}{d x}\) = \(\frac{1}{1+x^{2}}\)
Differentiating again with respect to x;
\(\frac{d^{2} y}{d x^{2}}\) = \(-\frac{1}{\left(1+x^{2}\right)^{2}} \cdot 2 x\).

Question 11.
Match the following. (4)

Answer:

Question 12.
If x – sint and y = sinmt show that
(i) y = sin(m sin^-1x) (1)
(ii) \(\frac{d y}{d x}\) (1)
(iii) (1 – x²) y₂ – xy₁ + m²y = 0 (2)
Answer:
(i) x = sint, y = sinmt
t = sin^-1x ⇒ y = sin(msin^-1x).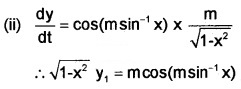

multiplying with \(\sqrt{1-x^{2}}\)
(1 – x²) y₂ – xy₁ = -m²y
(1 – x²) y₂ – xy₁ + m²y = 0.

Question 13.
Consider the function f(x) = x(x – 2), x ∈ [1, 3]. Verify mean value theorem for the function in[1, 3].
Answer:
f(x) = x(x – 2) = x² – 2x ⇒ f'(x) = 2x – 2.
As f is a polynomial, it is continuous in the interval [1, 3] and differentiable in the interval (1, 3).
Therefore two conditions of MVT are satisfied and so there exists c ∈ (1,3)such that.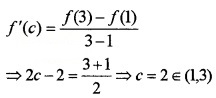

Hence MVT is verified.

Question 14.
Verify Lagranges’ Mean value theorem for the function f(x) = 2x² – 10x + 29 in [2, 9]
Answer:
f(x) = 2x² – 10x + 29; f'(x) = 4x – 10.
As f is a polynomial, it is continuous in the interval [2, 9] and differentiable in the interval (2, 9).
Therefore two conditions of MVT are satisfied and so there exists c ∈ (2, 9) such that.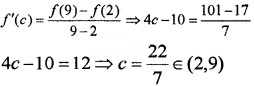

Hence MVT is verified.

Question 15.
Let f(x) = x(x – 1)(x – 2), x ∈ [0, 2]

1. Find f(0) and f(2) (1)
2. Find f'(x) (1)
3. Find the values of x when f'(x) = 0 verify Rolle’s theorem. (2)

Answer:
1. f(0) = 0, f(2) = 2(2 – 1)(2 – 2) = 0

2. We have, f(x) = x³ – 3x² + 2x
⇒ f'(x) = 3x² – 6x + 2.

3. f'(x) = 3x² – 6x + 2 = 0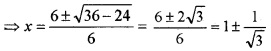

Clearly all the three conditions of Rolle’s theorem are satisfied and 1 ± \(\frac{1}{\sqrt{3}}\) ∈ (0, 2).

Question 16.
Verify Rolle’s Theorem for the function
f(x) = x² + 2x – 8, x ∈ [-4, 2]
Answer:
f(x) = x² + 2x – 8, f'(x) = 2x + 2.
As f is a polynomial, it is continuous in the interval [-4, 2] and differentiable in the interval (-4, 2).
f(-4) = 16 – 8 – 8 = 0
f(2) = 4 + 4 – 8 = 0
f'(c) = 0 ⇒ 2c + 2 = 0 ⇒ c = -1 ∈ (-4, 2) Hence Rolle’s Theorem is verified.

Question 17.
Examine that Rolle’s Theorem is applicable to the following function in the given intervals, justify your answer.

1. f(x) = [x], x ∈ [5, 9]
2. f(x) = x² – 1, x ∈ [1, 2]

Answer:
1. The function f(x) = [x] is not differentiable and continuous at integral values. So in the given interval [5, 9] the function is neither differentiable nor continuous at x = 6, 7 ,8. Therefore Rolle’s Theorem is not applicable.

2. The function f(x) = x² – 1 is a polynomial function so differentiable and continuous.
f(1) = 1 – 1 = 0, f(2) = 4 – 1 = 3
f(1) ≠ f(2) . Therefore Rolle’s Theorem is not applicable.

Question 18.
Examine the continuity of the function
\(f(x)=\left\{\begin{array}{cc}{|x|+3,} & {x \leq-3} \\{-2 x,} & {-3<x<3} \\{6 x+2,} & {x \geq 3}\end{array}\right.\)
Answer:
In the intervals x ≤ -3, f(x) is the sum of a constant function and modulus function so continuous. In the intervals -3 < x < 3 and x ≥ 3the function f(x) is a polynomial so continuous. Hence we have to check the continuity at x = -3, x = 3.
At x = -3
f(-3) = 6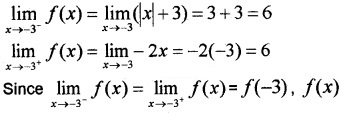

f(x) is continuous at x = -3.
At x = 3
f(3) = 6(3) + 2 = 20

Since \(\lim _{x \rightarrow 3^{-}}\)f(x) = f(3), f(x) is not continuous at x = 3.

Question 19.
Test continuity for the following functions.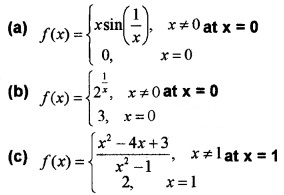

Answer: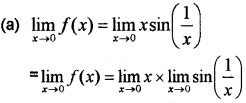

= 0 × a finite quantity between -1 and 1 = 0 Also f(0) = 0
Therefore f(x) is continuous at x = 0.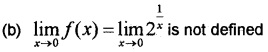

Therefore f(x) is discontinuous at x = 0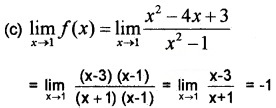

But f(1) = 2
∴ f(x) is discontinuous at x = 1.

Question 20.
If y = \(\frac{\sin ^{-1} x}{\sqrt{1-x^{2}}}\) prove that
(i) (1 – x²) y² = (sin^-1x)² (1)
(ii) (1 – x²)y₁ – xy = 1 (1)
(iii) (1 – x²) y₂ – 3xy₁ – y = 0 (2)
Answer: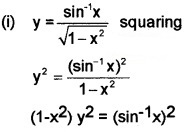

(ii) Differentiating
(1 – x²) 2y.y₁ + y²x – 2x = \(\frac{2 \sin ^{-1} x}{\sqrt{1-x^{2}}}\)
(1 – x²)2yy₁ – 2xy² = 2y
(1 – x²) y₁ – xy = 1.

(iii) Again differentiating
(1 – x²) y₂ + y₁ x – 2x – xy₁ – y = 0
(1 – x²) y₂ – 3xy₁ – y = 0.

Question 21.
At what point on the curve y = x², x ∈ [-2, 2] at which the tangent is parallel to x-axis?
Answer:
Y = x², a continuous function on [-2, 2] and differentiable on [-2, 2] f(2) = 4 = f(-2). All conditions of Rolles theorem is satisfied. Given the tangent is parallel to x-axis.
f¹ (x) = 2x
f¹(c) = 2c
f¹(c) = 0 ⇒ 2c = 0 ⇒ c = 0 ∈ [-2, 2]
where c = 0, y = 0
Therefore (0, 0) is the required point.

Question 22.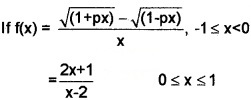

is continuous in the interval [-1 1].
(a) Find \(\lim _{x \rightarrow 0}\)f(x) (2)
(b) Find f(0). (1)
(c) Find P. (1)
Answer:

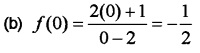
(c) Since f is continuous in [-1 1] it is continuous at 0.
Therefore P = \(-\frac{1}{2}\).

Question 23.
If ax² + 2hxy + by² = 1

1. Find \(\frac{d y}{d x}\) (1)
2. Find \(\frac{d^{2} y}{d x^{2}}\) (3)

Answer:
1. We have, ax² + 2hxy + by² = 1 ___(1)
Differentiating w.r.t.x, we get,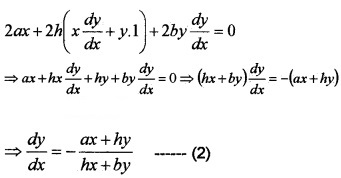

2. Differentiating (2) w.r.tx, we get,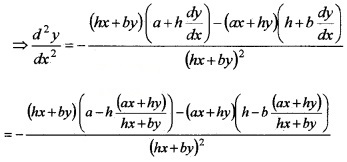

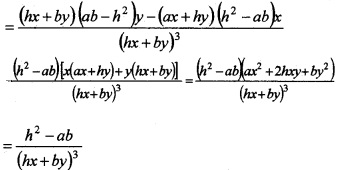
Question 24.
Consider the function y = x^x \(\sqrt{x}\)

1. Express the above function as logy = \(\left(x+\frac{1}{2}\right)\) logx (2)
2. Find \(\frac{d y}{d x}\) (2)

Answer:
1. Given, y = x^x \(\sqrt{x}\). Take log on both sides,

2. We have, logy = \(\left(x+\frac{1}{2}\right)\) logx
Differentiating w.r.t x, we get,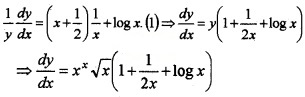

Plus Two Maths Continuity and Differentiability Six Mark Questions and Answers

Question 1.

1. Verify mean value theorem for the function f(x) = (x – 2)² in [1, 4].
2. Find a point on the curve y = (x – 2)² at which the tangent is parallel to the chord joining the points (1, 1) and (4, 2)
3. Find a point on the above curve at which the tangent is parallel to the x-axis.

Answer:
1. f(x) = (x – 1)², x ∈ [1, 4]
f(x) is continuous in [1, 4]
f'(x) = 2(x – 2) is differentiable in [1, 4]
Then there exists c ∈ [1, 4] so that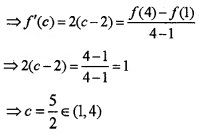

Hence Mean Value Theorem is verified.

2. c = \(\frac{5}{2}\) will be the x-coordinate to the point of contact of tangent and the curve, then y = (x – 2)² ⇒ y = (\(\frac{5}{2}\) – 2)² = \(\frac{1}{4}\)
Therefore the point is (\(\frac{5}{2}\), \(\frac{1}{4}\)).

3. The tangent parallel to x- axis will have
f'(c) = 0 ⇒ 2(c – 2) = 0 ⇒ c = 2
Then; x = 2 ⇒ y = (2 – 2)² = 0
Therefore the point is (2, 0).

Question 2.

1. Differentiate x^sinx w.r.t.x (2)
2. If x = at², y = 2at, then find \(\frac{d y}{d x}\) (2)
3. If y = sin^-1(cosx) + cos^-1(sinx), then find \(\frac{d y}{d x}\). (2)

Answer:
1. Let y = x^sinx, take log on both sides,
log y = sinx logx differentiate w. r.t.x, we get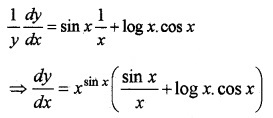

2.

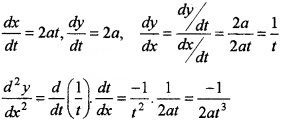
3. Given, y = sin^-1(cosx) + cos^-1(sinx)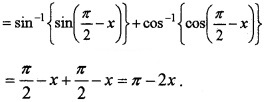

Differentiate w.r.t. x, we get \(\frac{d y}{d x}\) = -2.

Question 3.

1. Differentiate \(\frac{x-1}{x-3}\) with respect to x.(2)
2. Differentiate \(\sqrt{\frac{(x-1)(x-2)}{(x-3)(x-4)(x-5)}}\) with respect to x. (4)

Answer:
1. Let y = \(\frac{x-1}{x-3}\) Differentiate w.r.t. x, we get;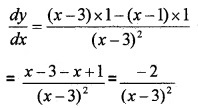

2. Given, y = \(\sqrt{\frac{(x-1)(x-2)}{(x-3)(x-4)(x-5)}}\)
Take log on both sides;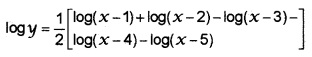

Differentiate w.r.t. x, we get;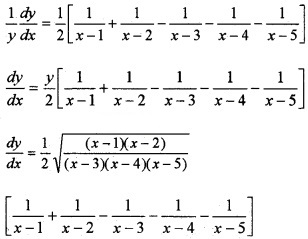

Question 4.
(i) Define |x|
(a) |x| = \(\sqrt{x^{2}}\)
(b) |x| = x
(c) |x| = -x
(d) |x| = x²
(ii) At which point \(\frac{d}{d x}\)|x| does not exist?
Find \(\frac{d}{d x}\) |x|. (2)
(iii) Find \(\frac{d}{d x}\)|x³ – 7x| . Also, find the point at which the derivative exists. (3)
Answer:
(i) (a) |x| = \(\sqrt{x^{2}}\).

(ii) At x = 0, \(\frac{d}{d x}\) |x| does not exist.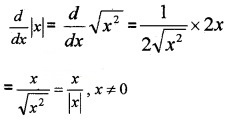

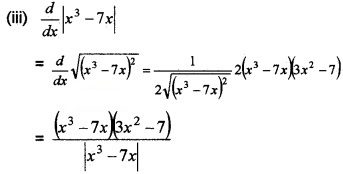
Does not exist at
x³ – 7x = 0 ⇒ x(x² – 7) = 0
⇒ x = 0, x² – 7 = 0 ⇒ x = ±\(\sqrt{7}\).

Question 5.
(i) Match the following (4)

(ii) If log (x² + y²) = 2 tan^-1\(\left(\frac{y}{x}\right)\), then, show that \(\frac{d y}{d x}=\frac{x+y}{x-y}\) (2)
Answer:
(i)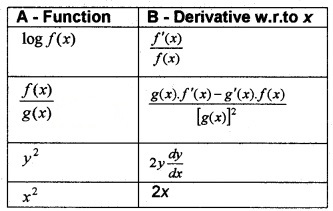

(ii) Given, log (x² + y²) = 2 tan^-1\(\left(\frac{y}{x}\right)\).
Differentiate w.r.to x, we get;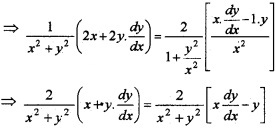

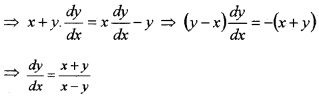
Question 6.
If x = a sec³θ and y = a tan³θ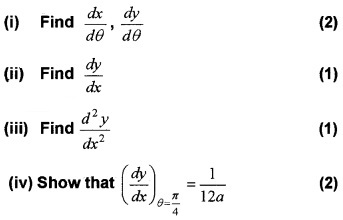

Answer:
(i) Given, x = a sec³θ
Differentiate w.r.to θ, we get;
\(\frac{d x}{d \theta}\) = 3a sec²θ. secθ. tanθ = 3a sec³ θ. tan θ
Given, y = a tan³θ .
Differentiating w.r.to θ, we get
\(\frac{d x}{d \theta}\) = 3a tan² θ. sec²θ.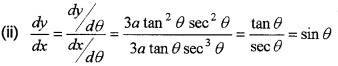

(iii) We have, \(\frac{d y}{d x}\) = sinθ
Differentiating w.r.to x, we get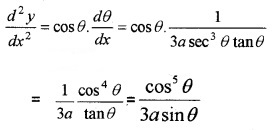

(iv) We have,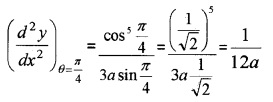

Question 7.
Consider the function \(f(x)=\left\{\begin{array}{cc}{1-x} & {, \quad x<0} \\{1} & {x=0} \\ {1+x} & {, \quad x>0}\end{array}\right.\)
(i) Compete the following table. (2)

(ii) Draw a rough sketch of f (x). (2)
(iii) What is your inference from the graph about Its continuity. Verify your answer using limits. (2)
Answer:

Since, f (- 2) = 1 – (- 2) = 3, f (-1) = 1 – (-1) = 2,
f(1) = 1 + (1) = 2, f (2) = 1 + (2) = 3.

(ii)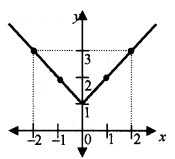

(iii) From the graph we can see that there is no break or jump at x = 0. Therefore continuous.
From the figure we can see that
f(0^–) = 1 f(0⁺) = 1 and f(0) = 1
Hence, f(0^–) = f(0⁺) = f(0) = 1.
Therefore continuous.

Question 8.
Consider the equation \(\sqrt{1-x^{2}}+\sqrt{1-y^{2}}=a(x-y)\)
(i) Simplify the above equation to sin^-1x – sin^-1y = 2cot^-1 a by giving suitable substitution.
(ii) Prove that \(\frac{d y}{d x}=\sqrt{\frac{1-y^{2}}{1-x^{2}}}\)
Answer: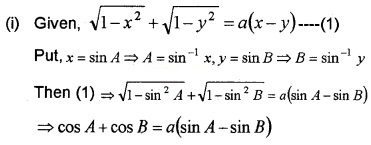

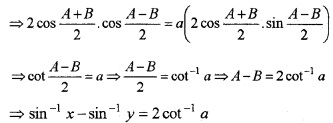
(ii) We have; sin^-1 x – cos^-1y = 2cot^-1a.
Differentiating w.r.t x, we get,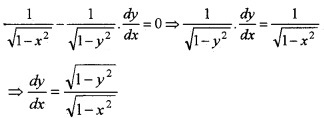

Question 9.
(i) Match the following. (4)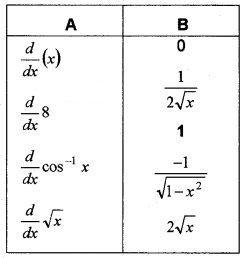

(ii) If y = e^{a cos-1x}, then show that (1 – x²)y₂ – xy₁ – a²y = 0 (2)
Answer:
(i)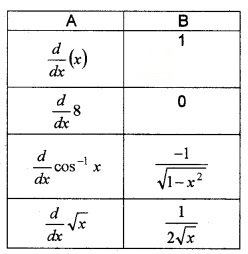

(ii) Given, y = e^{a cos-1x} ____(1)
Differentiating w.r.to x,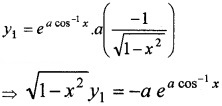

Again differentiating w. r.to x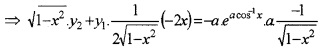

⇒ (1 – x²)y₂ – xy₁ = a². e^{a cos-1x}
⇒ (1 – x²)y₂ – xy₁ = a²y
⇒ (1 – x²)y₂ – xy₁ – a²y = 0.

Question 10.
(i) Match the following (3)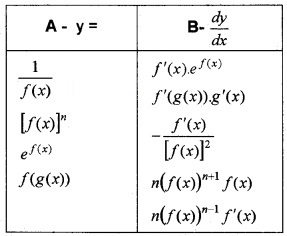

Differentiate the following
(ii) y =\(\frac{1}{5 x^{2}+3 x+7}\) (1)
(iii) y = 3cosec⁴(7x) (1)
(iv) y = e^{2log tan 5x} (1)
Answer:
(i)

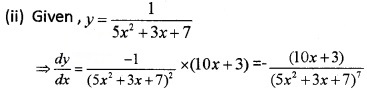
(iii) Given,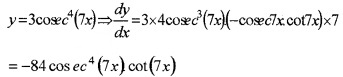

(iv) Given,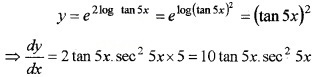

Plus Two Mathematics All Chapters Question and Answers

• Plus Two Mathematics Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 1 Relations and Functions Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 2 Inverse Trigonometric Functions Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 3 Matrices Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 4 Determinants Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 5 Continuity and Differentiability Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 6 Application of Derivatives Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 7 Integrals Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 8 Application of Integrals Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 9 Differential Equations Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 10 Vector Algebra Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 11 Three Dimensional Geometry Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 12 Linear Programming Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 13 Probability Chapter Wise Question and Answers PDF

Benefits of the Plus Two Maths Chapter 5 Continuity and Differentiability Chapter Wise Question and Answers PDF

The Plus Two Maths Chapter 5 Continuity and Differentiability Chapter Wise Question and Answers PDF that has been provided above is extremely helpful for all students because of the way it has been drafted. It is designed by teachers who have over 10 years of experience in the field of education. These teachers use the help of all the past years’ question papers to create the perfect Plus Two Maths Chapter 5 Continuity and Differentiability Chapter Wise Question and Answers PDF.

FAQ’s Plus Two Maths Chapter 5 Continuity and Differentiability Chapter Wise Question and Answers PDF

Where can I download Plus Two Maths Chapter 5 Continuity and Differentiability Chapter Wise Question and Answers PDF?

You can download Plus Two Maths Chapter 5 Continuity and Differentiability Chapter Wise Question and Answers PDF for the latest 2021 session.

Can I download Plus Two All subjects Question and Answers PDF?

Yes - You can click on the links above and download subject wise question papers in PDF

Is there any charge for the Plus Two Maths Chapter 5 Continuity and Differentiability Chapter Wise Question and Answers PDF?

There is no charge for the model papers for you can download everything free