Plus Two Maths Chapter 6 Application of Derivatives Chapter Wise Question and Answers PDF Download

Plus Two Maths Chapter 6 Application of Derivatives Chapter Wise Question and Answers PDF Download: Students of Standard 12 can now download Plus Two Maths Chapter 6 Application of Derivatives chapter wise question and answers pdf from the links provided below in this article. Plus Two Maths Chapter 6 Application of Derivatives Question and Answer pdf will help the students prepare thoroughly for the upcoming Plus Two Maths Chapter 6 Application of Derivatives exams.

Plus Two Maths Chapter 6 Application of Derivatives Chapter Wise Question and Answers

Plus Two Maths Chapter 6 Application of Derivatives question and answers consists of questions asked in the previous exams along with the solutions for each question. To help them get a grasp of chapters, frequent practice is vital. Practising these questions and answers regularly will help the reading and writing skills of students. Moreover, they will get an idea on how to answer the questions during examinations. So, let them solve Plus Two Maths Chapter 6 Application of Derivatives chapter wise questions and answers to help them secure good marks in class tests and exams.

Board	Kerala Board
Study Materials	Chapter wise Question and Answers
For Year	2021
Class	12
Subject	Mathematics
Chapters	Maths Chapter 6 Application of Derivatives
Format	PDF
Provider	Spandanam Blog

How to check Plus Two Maths Chapter 6 Application of Derivatives Question and Answers?

1. Visit our website - https://spandanamblog.com
2. Click on the 'Plus Two Question and Answers'.
3. Look for your 'Plus Two Maths Chapter 6 Application of Derivatives Question and Answers'.
4. Now download or read the 'Class 12 Maths Chapter 6 Application of Derivatives Question and Answers'.

Plus Two Maths Chapter 6 Application of Derivatives Question and Answers PDF Download

We have provided below the question and answers of Plus Two Maths Chapter 6 Application of Derivatives Chapter wise study material which can be downloaded by you for free. These Plus Two Maths Chapter 6 Application of Derivatives Chapter Wise Question and answers will contain important questions and answers and have been designed based on the latest Plus Two Maths Chapter 6 Application of Derivatives, books and syllabus. You can click on the links below to download the Plus Two Maths Chapter 6 Application of Derivatives Chapter Wise Question and Answers PDF. 

Question 1.
Find the equation of tangents and normals to the given curves x = cost, y = sin t at t = \(\frac{π}{4}\).
Answer:
Given; x = cost, y = sin t

Equation of tangent at t = \(\frac{π}{4}\) is;

Equation of normal at t = \(\frac{π}{4}\) is;

⇒ \(\sqrt{2}\)y + \(\sqrt{2}\)x = 0 ⇒ y + x = 0.

Question 2.
A ladder Sm long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2cm/s. How fast is its height on decreasing when the foot of the ladder is 4m away from the wall?
Answer:
From the figure we have;
x² + y² = 25 ____(1)

Differentiating w.r.t t;

From (1) when x = 4 ⇒ 16 + y² = 25 ⇒ y = 3
Given; \(\frac{d x}{d t}\) = 2cm/s = 0.02 m/s
(2) ⇒ 4(0.02) + 3 \(\frac{d x}{d t}\) = 0

Question 3.
Find the points on the curve y = x³, the tangents at which are inclined at an angle of 60° to x-axis?
Answer:
\(\frac{d y}{d x}\) = 3x²
Slope of the tangent = tan60°
i.e. 3x² = \(\sqrt{3}\)

Question 4.
Find the equation of the tangent to the parabola y² = 4x + 5 which is parallel to y = 2x + 7.
Answer:
y² = 4x + 5 _____(1)
2y \(\frac{d y}{d x}\) = 4
\(\frac{d y}{d x}\) = \(\frac{4}{2y}\) = \(\frac{2}{y}\)
Given tangent is parallel to y = 2x + 7
ie. Slope of the tangent is 2 ⇒ \(\frac{2}{y}\) = 2 ⇒ y = 1
∴ from (1) ⇒ 1 = 4x+ 5 ⇒ 4x = -4 ⇒ x = -1
So the point of contact is (-1, 1).
∴ Equation of tangent is
y -1 = 2(x + 1) ⇒ y = 2x + 3.

Question 5.
Find the intervals in which the function f given f(x) = 2x² – 3x is

1. Strictly increasing.
2. Strictly decreasing.

Answer:
Given; f(x) = 2x² – 3x ⇒ f'(x) = 4x – 3
For turning points; f'(x) = 0
⇒ 4x – 3 = 0 ⇒ x = \(\frac{3}{4}\)
The intervals are \(\left(-\infty, \frac{3}{4}\right),\left(\frac{3}{4}, \infty\right)\)
f'(0) = – 3 < 0
∴ Strictly decreasing in \(\left(-\infty, \frac{3}{4}\right)\)
f'(1) = 1 > 0
∴ Strictly increasing in \(\left(\frac{3}{4}, \infty\right)\).

Question 6.
Find the intervals in which the function f(x) = (x + 1)³ (x – 3)³ strictly increasing or decreasing.
Answer:
Given; f(x) = (x + 1)³ (x – 3)³
⇒ f'(x) = (x + 1)³ 3(x – 3)² + (x – 3)³3(x + 1)²
= 3(x + 1)²(x – 3)²(x + 1 + x – 3)
= 3(x + 1)²(x – 3)²(2x – 2)
= 6(x +1)² (x – 3)² (x -1)
⇒ 6(x +1)² (x – 3)² (x – 1) = 0
⇒ x = -1, 1, 3
The intervals are
(-∞, -1), (-1, 1), (1, 3), (3, ∞)
f'(-2) = (-2 – 1) < 0
∴ Strictly decreasing in (-∞, -1)
f'(0) = (0 – 1) < 0
∴ Strictly decreasing in (-1, 1)
f'(2) = (2 – 1) > 0
∴ Strictly increasing in (1, 3)
f'(4) = (4 – 1) > 0
∴ Strictly increasing in (3, ∞).

Question 7.
Find the intervals in which the function f(x) = x + \(\frac{1}{x}\) strictly increasing or decreasing.
Answer:

⇒ x = ±1
The intervals are (-∞, -1), (-1, 1), (1, ∞)
f'(-2) > 0
∴ Strictly increasing in (-∞, -1)
f'(0) < 0
∴ Strictly decreasing in (-1, 1)
f'(2) > 0
∴ Strictly increasing in (1, ∞).

Question 8.
Determine whether the f(x) = x² function is strictly monotonic on the indicated interval.

1. (-1, 1)
2. (-1, 0)
3. (0, 1)

Answer:
f(x) = x²
⇒ f'(x) = 2x
⇒ f'(x) = 0 ⇒ 2x = 0 ⇒ x = 0
This turning point divides the domain into the intervals (-∞, 0); (0, ∞).

1. Interval (-1, 1) f'(x) < 0 and f'(x) > 0. So f(x) is not monotonic.
2. Interval (-1, 0), f'(x) < 0. ∴ f(x) is strictly monotonic.
3. Interval (0, 1) f'(x) > 0 and f(x) is strictly monotonic.

Question 9.
Determine whether the f(x) = x³ – x function is strictly monotonic on the indicated interval.

1. (-1, 0)
2. (-1, -1/2)
3. (-1, 1)

Answer:
(x) = x³ -x ⇒ f'(x) = 3x² – 1
⇒ f'(x) = 0 ⇒ 3x² – 1 = 0 ⇒ x = ±\(\frac{1}{\sqrt{3}}\)
This turning point divides the domain into the intervals (-∞, \(\frac{1}{\sqrt{3}}\)); (-\(\frac{1}{\sqrt{3}}\), \(\frac{1}{\sqrt{3}}\)); (\(\frac{1}{\sqrt{3}}\), ∞).

1. Interval (-1, 0), f'(x) changes sign. So not monotonic.
2. Interval (-1, -1/2), f'(x) > 0 strictly monotonic.
3. lnterval(-1, 1) not monotonic

Question 10.
Find the approximate change in the volume V of a cube of side x meters caused by increasing the side by 1%.
Answer:
We have; V = x³ and ∆x = 1% of x= 0.01x
dV = \(\frac{d V}{d x}\) ∆x = 3x²∆x
= 3x² × 0.01x = 0.03x³ = 0.03V
⇒ \(\frac{d V}{V}\) = 0.03
Therefore 3% is the approximate increase in volume.

Question 11.
If the radius of a sphere is measured as 7m with an error of 0.02m then find the approximate error in calculating its volume.
Answer:
Let r be the radius of the sphere and ∆r be the error in measuring the radius then r =7m and ∆r = 0.02 m
We have; V = \(\frac{4}{3}\) πr³
dV = \(\frac{d V}{dr}\) ∆r = \(\frac{4}{3}\) π3r² × ∆r
= 4π(7)² × 0.02 = 3.92 π m³.

Question 12.
The length of a rectangle is decreasing at the rate of 5 cm/min and the width is increasing at the rate of 4cm/min. When length is 8 cm and width is 6 cm, find the rate of change of its area.
Answer:
Let length = x and width = y

Question 13.
Find the equation of tangents and normals to the given curves y= x⁴ – 6x³ + 13x² – 10x + 5 at (0, 5)
Answer:
Given; y = x⁴ – 6x³ + 13x² – 10x + 5 at (0, 5)
⇒ \(\frac{d y}{d x}\) = 4x³ – 18x² + 26x – 10
Slope = \(\left(\frac{d y}{d x}\right)_{x=0}\) = -10
Equation of tangent at (0, 5) is;
y – 5 =(-10)(x – 0)
⇒ y – 5 = -10x ⇒ 10x + y – 5 = 0
Equation of normal at (0, 5) is;
y – 5 = \(\frac{1}{10}\)(x – 0)
⇒ 10y – 50 = x ⇒ x – 10y + 50 = 0.

Question 14.
Find the equation of tangents and normals to the given curves y = x³ at (1, 1)
Answer:
Given; y = x³
⇒ \(\frac{d y}{d x}\) = 3x²
Slope = \(\left(\frac{d y}{d x}\right)_{x=1}\) = 3
Equation of tangent at (1, 1) is; y -1 = (3)(x – 1)
⇒ y – 1 = 3x – 3 ⇒ 3x – y – 2 = 0
Equation of normal at (1, 1) is;
y – 1 = \(-\frac{1}{3}\)(x – 1)
⇒ 3y – 3 = -x + 1 ⇒ x+ 3y – 4 = 0.

Question 15.
The volume of a cube is increasing at the rate of 8cm³/s. How fast is the surface area increasing when the length of an edge is 12cm.
Answer:
Let V be the volume of the cube of side x.
We have volume = V = x³
Rate of change of volume with respect to time ‘t’ is;
ie; differentiating w.r.t t; \(\frac{d V}{d t}\) = 3x²\(\frac{d x}{d t}\)
Given; \(\frac{d V}{d t}\) = 8 and x = 12 ⇒ 8 = 3(12)²\(\frac{d x}{d t}\)

Now let Surface area = S = 6x²
Differentiating w.r.t t;

Question 16.
Find the intervals in which the function f(x) = -2x³ – 9x² – 12x + 1 strictly increasing or decreasing.
Answer:
Given; f(x) = -2x³ – 9x² – 12x + 1
⇒ f'(x) = -6x² – 18x – 12
= – 6(x² + 3x + 2)
= – 6(x + 2)(x +1)
⇒ f'(x) = 0 ⇒ -6(x + 2)(x +1) = 0
⇒ x = -2, -1
The intervals are (-∞, -2),(- 2, -1),(-1, ∞)
f'(-3) = -(-3 + 2)(-3 + 1) < 0
∴ Strictly decreasing in (-∞, -2)
f'(-1.5) = -(-1.5 + 2)(-1.5 + 1) > 0
∴ Strictly increasing in (- 2, -1)
f'(0) = -(0 + 2)(0 + 1) < 0
Strictly decreasing 1n(-1, ∞).

Question 17.
Find the local maxima and minima of the following functions. Also find the local maximum and minimum values. (each question carry 3 score)

1. f(x) = sin x + cosx, 0 < x < \(\frac{\pi}{2}\)
2. f(x) = x³ – 3x
3. f(x) = x³ – 6x² + 9x + 15
4. g(x) = \(\frac{x}{2}\) + \(\frac{2}{x}\), x > 0
5. g(x) = \(\frac{1}{x^{2}+2}\)

Answer:
1. Given; f(x) = sinx + cosx
⇒ f'(x) = cosx – sinx
For turning point f'(x) = 0
⇒ cosx – sinx = 0
⇒ cosx = sinx
⇒ x = \(\frac{\pi}{4}\)
f”(x) = -sin x – cosx
⇒ f (\(\frac{\pi}{4}\)) = -sin\(\frac{\pi}{4}\) – cos\(\frac{\pi}{4}\) < 0
Hence f(x) has a local maximum at x = \(\frac{\pi}{4}\) and local maximum value is

2. Given; f(x) = x³ – 3x
⇒ f'(x) = 3x² – 3
For turning point f'(x) = 0
⇒ 3x² – 3 = 0
⇒ x = ±1
f”(x) = 6x
When x = -1
⇒ f”(-1) = -6 < 0
Hence f(x) has a local maximum at x = -1 and local maximum value is
f(-1) = (-1)³ – 3(-1) = -1 + 3 = 2
When x = 1
⇒ f”(1) = 6 > 0
Hence f(x) has a local minimum at x = 1 and local minimum value is
f(1) = (1)³ – 3(1) = 1 – 3 = -2.

3. Given; f(x) = x³ – 6x² + 9x + 15
⇒ f'(x) = 3x² – 12x + 9
For turning point f'(x) = 0
⇒ 3x² – 12x + 9 = 0 ⇒ 3(x² – 4x + 3) = 0
⇒ 3(x – 1)(x – 3) = 0 ⇒ x = 1, 3
f”(x) = 6x – 12
When x = 1
⇒ f”( 1) = 6 – 12 < 0
Hence f(x) has a local maximum at x = 1 and local maximum value is
f(1) = (1)³ – 6(1)² + 9(1) + 15 = 19
When x = 3
⇒ f”(3) = 6(3) – 12 > 0
Hence f(x) has a local minimum at x = 3 and local minimum value is
f(3) = (3)³ – 6(3)² + 9(3) + 15 = 15.

4. Given; g(x) = \(\frac{x}{2}\) + \(\frac{2}{x}\)
⇒ g'(x) = \(\frac{1}{2}\) – \(\frac{2}{x^{2}}\)
For turning point g'(x) = 0

Since x > 0, the acceptable value of x = 2

Hence g(x) has a local maximum at x = 2 and local maximum value is g(2) = \(\frac{2}{2}\) + \(\frac{2}{2}\) = 2

5. Given; g(x) = \(\frac{1}{x^{2}+2}\)

For turning point g'(x) = 0


Hence g(x) has a local maximum at x = 2 and maximum value is g(2) = \(\frac{1}{0+2}=\frac{1}{2}\).

Question 18.
Find the absolute maximum value and minimum value of the following functions.

1. f(x) = x³, x ∈ [-2, 2]
2. f(x) = 4x – \(\frac{x^{2}}{2}\), x ∈ \(\left[-2, \frac{9}{2}\right]\)

Answer:
1. Given; f(x) = x³ ⇒ f'(x) = 3x²
For turning point f'(x) = 0 ⇒ 3x² = 0 ⇒ x = 0
f(- 2) = (-2 )³ = -8
f( 2) = (2)³ = 8
f(0) = (0)³ = 0
Absolute maximum = max{-8, 8, 0} = 8
Absolute minimum = min {-8, 8, 0} = – 8

2. Given; f(x) = 4x – \(\frac{x^{2}}{2}\) ⇒ f'(x) = 4 – x
For turning point f'(x) = 0 ⇒ 4 – x = 0
⇒ x = 4

Absolute maximum = max{-10, 8, 7.875} = 8
Absolute minimum = min {-10, 8, 7.87} = -10.

Question 19.
A television camera at ground level is filming the lift-off of a space shuttle that is rising vertically according to position equation S = 50t².
The camera is 2000 feet from the launch pad. Find the rate of change in the angle of elevation of the camera 10 seconds after lift-off.
Answer:

Question 20.
Determine whether the f(x) = sinx function is strictly monotonic on the indicated interval.

1. (0, 2π)
2. (0, π)
3. (-π/2, π/2)

Answer:
f(x) = sinx ⇒ f'(x) = cosx changes sign.

1. Interval (0, 2π). ∴ f(x) is not monotonic.
2. f'(x) changes sign in (0, π) not monotonic.
3. f'(x) > 0 in (-π/2, π/2), ie. f(x) is strictly monotonic.

Question 21.
Find the approximate change in the Surface Area of a cube of side x meters caused by decreasing the side by 1%.
Answer:
We have;
S = 6x² and ∆x = 1% of x = -0.01x
dS = \(\frac{d S}{d x}\) ∆x = 6 × 2x × ∆x
= 6 × 2x × -0.01x = -0.02 × 6x² = -0.02S
⇒ \(\frac{d S}{S}\) = -0.02
Therefore 2% is the approximate decrease in surface area.

Plus Two Maths Application of Derivatives Four Mark Questions and Answers

Question 1.
The length ‘x’ of a rectangle is decreasing at the rate of 2 cm/s and the width ‘y’ is increasing at the rate of 2 cm/s.

1. Find the rate of change of the Perimeter.
2. Find \(\frac{d A}{dt}\) when x = 12 cm and y = 5 cm.

Answer:
Since the length ‘x’ is decreasing and the width ‘y’ is increasing, we have \(\frac{d x}{dt}\) = -2 cm/s and \(\frac{d y}{dt}\)
= 2 cm/sec.
1. The Perimeter ‘P’ of the rectangle is given by
P = 2 (x + y)

2. The area ‘A’ of the rectangle ‘A’ is given by
A = x.y

= 12(2) + 5(-2)
= 24 – 10 = 14 cm2/s.

Question 2.
Find the equation of all lines having slope -1. Which are tangents to the curve?
y = \(\frac{1}{x-1}\), x ≠ 1
Answer:

⇒ x² – 2x = 0 ⇒ x(x – 2) = 0 ⇒ x = 0, x = 2
At x = 0, y = -1
Equation of tangent at (0, -1) is;
At x = 2, y = \(\frac{1}{2-1}\) = 1
Equation of tangent at (2, 1) is; y – 1 = -1(x – 2)
⇒ y – 1 = -x + 2 ⇒ x + y – 3 = 0.

Question 3.
Find the points on the curve x² + y² – 2x – 3 = 0 at which the tangent are parallel to x-axis.
Answer:
Given; x² + y² – 2x – 3 = 0
Differentiating with respect to x;

Since the tangent is parallel to x-axis \(\frac{d y}{d x}\) = 0
\(\frac{1-x}{y}\) = 0 ⇒ x = 1
We have; (1)² + y² – 2(1) – 3 = 0
⇒ y² = 4 ⇒ y = ±2
Hence the points are (1, 2), (1, -2).

Question 4.
Find the equation of the tangent to the curve y = \(\sqrt{3 x-2}\) which is parallel to the line 4x – 2y + 5 = 0.
Answer:
Slope of the line 4x – 2y + 5 = 0 is 2.

acceptable since y is positive.
Hence the point is \(\left(\frac{41}{48}, \frac{3}{4}\right)\)
Equation of tangent is;

⇒ 6(4y – 3) = (48x – 41)
⇒ 24y – 18 = 48x – 41
⇒ 48x – 24y – 23 = 0.

Question 5.
Prove that the curve x = y² and xy = k cut at right angles, if 8k² = 1.
Answer:
x = y² ___(1)
⇒ 1 = 2y \(\frac{d y}{d x}\) ⇒ \(\frac{d y}{d x}\) = \(\frac{1}{2y}\)
xy = 2k ___(2)
⇒ x \(\frac{d y}{d x}\) + y.1 = 0 ⇒ \(\frac{d y}{d x}\) = \(-\frac{y}{x}\)
The product of the slopes will be – 1.

Question 6.
The gradient at any point (x, y) of a curve is 3x² – 12, and the curve through the point (2, -7).

1. Find the equation of the tangent at the point ( 2, -7 ). (2)
2. Find the equation to the curve. (2)

Answer:
1. Given gradient as 3x² – 12 ⇒ \(\frac{d y}{d x}\) = 3x² – 12
Slope at (2, -7) is given by
\(\left(\frac{d y}{d x}\right)_{x=2}\) = 3(2)² – 12 = 0
Since slope is zero, the tangent is parallel to x – axis.
Here y = – 7 is the equation of the tangent at (2, -7).

2. Given, \(\frac{d y}{d x}\) = 3x² – 12
⇒ ∫dy = ∫(3x² – 12 )dx
y = 3\(\frac{x^{3}}{3}\) – 12x + c ⇒ y = x³ – 12x + c ____(1)
Given (2, -7) is a point on the curve.
(1) ⇒ -7 = (2)³ – 12(2) + c ⇒ -7 = 8 – 24 + c ⇒ c = 9
∴ Curve is y = x³ – 12x + 9.

Question 7.
Consider the curve x^2/3 + y^2/3 = 2

1. Find the slope of the tangent to the curve at the point (1, 1). (2)
2. Find the equation of the normal at the point (1, 1). (2)

Answer:
1. Given, x^2/3 + y^2/3 = 2,
Differentiating w.r.t. x,

⇒ slope of tangent = – 1.

2. Slope of normal = \(-\frac{1}{-1}\) = 1.
Equation of the normal is
y – 1 = 1(x – 1) ⇒ y – x = 0.

Question 8.
Find the intervals in which the function f given by f(x) = 2x³ – 3x² – 36x + 7 is

1. Strictly increasing. (2)
2. Strictly decreasing. (2)

Answer:
Given; f(x) = 2x³ – 3x² – 36x + 7
⇒ f'(x) = 6x² – 6x – 36
f'(x) = 0 ⇒ 6x² – 6x – 36 = 0
⇒ 6(x² – x – 6) = 0
⇒ 6(x + 2)(x – 3) = 0 ⇒ x = -2, 3
The intervals are (-∞, -2),(- 2, 3), (3, ∞)
f'(-3) = 6(-3 + 2)(-3 – 3) > 0.
∴ Strictly increasing in (-∞, -2).
f'(0) = 6(2)(-3) < 0.
∴ Strictly decreasing in (- 2, 3).
f'(4) = 6(4 + 2)(4 – 3) > 0
∴ Strictly increasing in (3, ∞).

Question 9.
Use differentials to find the approximate value of \(\sqrt{0.6}\) up to 3 places of decimals.
Answer:
Take y = \(\sqrt{x}\), let x = 0.64 and ∆x = -0.04
Then; f(x) = y = \(\sqrt{x}\)
f(x + ∆x) = y + ∆y

(1) ⇒ \(\sqrt{0.6}\) = 0.8 – 0.025 = 0.775.

Question 10.
Use differentials to find the approximate value of (0.999)^{\(\frac{1}{10}\)} up to 3 places of decimals.
Answer:
Take = x^{\(\frac{1}{10}\)}, let x = 1 and ∆x = -0.001
Then; f(x) = y
f(x + ∆x) = y + ∆y
(0.999)^{\(\frac{1}{10}\)} = x^{\(\frac{1}{10}\)} + ∆y
(0.999)^{\(\frac{1}{10}\)} = (1)^{\(\frac{1}{10}\)} + ∆y
⇒ (0.999)^{\(\frac{1}{10}\)} = 1 + ∆y ______(1)

(1) ⇒ (0.999)^{\(\frac{1}{10}\)} = 1 – 0.0001 = 0.9999.

Question 11.
Use differentials to find the approximate value of (15)^{\(\frac{1}{4}\)} up to 3 places of decimals.
Answer:
Takey = x^{\(\frac{1}{4}\)}, let x = 16 and ∆x = -1
Then; f(x) = y
f(x + ∆x) = y + ∆y
(15)^{\(\frac{1}{4}\)} = x^{\(\frac{1}{4}\)} + ∆y
(15)^{\(\frac{1}{4}\)} = 16^{\(\frac{1}{4}\)} + ∆y
(15)^{\(\frac{1}{4}\)} = 2 + ∆y ____(1)
⇒ ∆y ≈ dy = \(\frac{d y}{d x}\) ∆x

Question 12.
Use differentials to find the approximate value of (26.57)^{\(\frac{1}{3}\)} up to 3 places of decimals.
Answer:
Take y = x^{\(\frac{1}{3}\)}, let x = 27 and ∆x = -0.43
Then; f(x) = y
f(x + ∆x) = y + ∆y
f(x + ∆x) = f(x) + ∆y
(26.57)^{\(\frac{1}{3}\)} = 27^{\(\frac{1}{3}\)} + ∆y .
⇒ (26.57)^{\(\frac{1}{3}\)} = 3 + ∆y ____(1)

(1) ⇒ (26.57)^{\(\frac{1}{3}\)} = 3 – 0.016 = 2.984.

Question 13.
Find the approximate value of f(5.001) where f(x) = x³ – 7x² + 15
Answer:
Let x = 5 and ∆x = 0.001
Then; f(x) = y
f(x + ∆x) = y + ∆y
f (5.001) = f(x) + ∆y
f(5.001) = f(5) + ∆y
f(5.001) = 5³ – 7(5)² + 15 + ∆y
⇒ f(5.001) = -35 + ∆y …
⇒ ∆y ≈ dy = \(\frac{d y}{d x}\) ∆x ⇒ dy = (3x² – 14x) × 0.001
= (3(5)² – 14(5)) × 0.001 = (75-70)0.001 = 0.005
(1) ⇒ f(5.001) = -35 + 0.005 = -34.995.

Question 14.
Find the approximate value of f(3.02) where f(x) = 3x² + 5x + 3
Answer:
Let x = 3 and ∆x = 0.02
Then; f(x) = y
f(x + ∆x) = y + ∆y
f(3.02) = f(x) + ∆y
f(3.02) = f(3) + ∆y
f(3.02) = 3(3)² + 5(2) + 3 + ∆y
⇒ f(3.02) = 45 + ∆y ____(1)
⇒ ∆y ≈ dy = \(\frac{d y}{d x}\) ∆x ⇒ dy = (6x + 5) × 0.02
= (6(3) + 5) × 0.02 = (18 + 5)0.02 = 0.46
(1) ⇒ f(3.02) = 45 + 0.46 = 45.46.

Question 15.
Consider the function y = f\(\sqrt{x}\)

1. If x = 0.0036 and ∆x = 0.0001 find ∆y. (3)
2. Hence approximate \(\sqrt{.0037}\) using differentials. (1)

Answer:
1. Let x = .0036, ∆x = 0.0001

2. (1) ⇒ \(\sqrt{.0037}\) = .000833 + .06 = .060833.

Question 16.
Find the approximate value of \(\sqrt[3]{124}\).
Answer:
f(x) = \(\sqrt[3]{x}\) = x^1/3 ⇒ f¹(x) = 1/3x^-2/3 = \(\frac{1}{3 x^{2 / 3}}\)
Let x = 125, ∆x = -1
Then; f(x) = y

Question 17.
Find two numbers x and y such that their sum is 35 and the product is x² y⁵ a maximum.
Answer:
Given; x + y = 35 ⇒ y = 35 – x
P = x² y⁵ ⇒ P = x²(35 – x)⁵
⇒ p’ = 2x(3 5 – x)⁵ + x² 5(35 – x)⁴(-1)
⇒ P’ = x(35 – x)⁴[2(35- x) – 5x]
⇒ p’ = x(35 – x)⁴[70 – 7x]
⇒ p’ = 7x(35 – x)⁴[10 – x]
⇒ p” = 7[x(3 5 – x)⁴ [-1] + x(10 – x)4(35 – x)³ (-1) + (35 – x)⁴(10 – x)]
For turning points P’ = 0
⇒ 7x(35 – x)⁴[10 – x] = 0
⇒ x = 0, 35, 10
x = 0, 35 can be rejected since correspondingly y will be y = 35, 0
⇒ P” = 7[10(35 – 10)⁴[-1]] < 0
Therefore maximum at x = 10
Thus the numbers are 10 and 35 – 10= 10.

Question 18.
Using differentials, find the approximate value of (63)^1/3.
Answer:
Take y = x^{\(\frac{1}{3}\)}, let x = 64 and ∆x = 1
Then; f(x) = y
f(x + ∆x) = y + ∆y

Question 19.

1. Find the point on the curve y = x³ – 10x + 8 at which the tangent is parallel to the line y = 2x + 1. (2)
2. Is the given line tangent to the curve? Why?

Answer:
1. \(\frac{d y}{d x}\) = 3x² – 10
Slope of the line y = 2x +1 is 2
⇒ 3x² – 10 = 2 ⇒ 3x² = 12 ⇒ x = ±2
When x = 2
y = 2³ – 10 × 2 + 8 = 8 – 20 + 8 = -4
When x = – 2
y = (-2)³ -10 × (-2) + 8 = -8 + 20 + 8 = 20
Therefore the points are (2, -4); (-2, 20)

2. No. Since (2, -4); (-2, 20) does not satisfies the equation y = 2x + 1.

Question 20.
Suppose that a spherical balloon is inflated and it has volume ‘v’ and radius ‘r’ at time ‘t’.

1. If the balloon is inflated by pumping 900c.c. of gas per second. Find the rate a which the radius of the balloon is increasing when the radius is 15 cm. (2)
2. Find the rate of change of its surface at the instant when it radius is 15 cm. (2)

Answer:
1. Let V be the volume of the sphere of radius r.
V = \(\frac{4}{3}\) πr³, given; \(\frac{d V}{d t}\) = 900, r = 15
Differentiating w.r.t t,

2. Let ‘s’ denote the surface area of the balloon, then
S = 4πr²
Differentiating, \(\frac{d s}{d t}\) = 4π.2r.\(\frac{d r}{d t}\) =8.π r .\(\frac{d r}{d t}\)
= 8π × 15 × \(\frac{1}{\pi}\) = 120 cm²/sec.

Question 21.
Use differentials to find the approximate value of (0.009)^{\(\frac{1}{3}\)} up to 3 places of decimals.
Answer:
Take y = x^{\(\frac{1}{3}\)}, let x = 0.008 and ∆x = 0.001
Then; F(x) = Y
f(x + ∆x) = y + ∆y

Question 22.
Find the approximate value of \(\sqrt{401}\).
Answer:
f(x) = \(\sqrt{x}\) = x^1/2
f'(x) = \(\frac{1}{2 \sqrt{x}}\)
Let x = 400 ∆x = 1
f(x) = y = \(\sqrt{x}\)
f(x + ∆x) = y + ∆y

Question 23.
Consider y = \(\frac{\log x}{x}\), in (0, ∞)

1. Find the value of x at which \(\frac{d y}{d x}\) = 0 (2)
2. Find the maximum value.

Answer:
1.

2.

∴ y is maximum when x = e.
The maximum value is \(\frac{1}{e}\).

Question 24.
Find the point on the curve y = x³ – 11x + 5 at which the tangent is y = x – 11.
Answer:
Slope of the line y = x – 11 is 1.
Given; y = x³ – 11x + 5 ⇒ \(\frac{d y}{d x}\) = 3x² – 11 = 1
⇒ 3x² = 12 ⇒ x = ±2
At x = 2, ⇒ y = x – 11 = 2- 11 = -9
⇒ (2, -9)
At x = -2, ⇒ y = x – 11 = -2 – 11 = -13
⇒ (-2, -13)
But the point (-2, -13) do not lie on the curve, hence the point is (2, -9).

Question 25.
Consider the curve y = x² – 2x + 7

1. Find the slope of the tangent of the curve at x = 2. (2)
2. Write down the equation of the tangent at x =2. (2)

Answer:
1. Given, y = x² – 2x + 7 ⇒ y’ = 2x – 2
(y’)_x=2 = 2(2) – 2 = 2.

2. At x = 2 , y = 2² – 2(2) + 7 = 7.
Equation of the tangent at (2, 7) is
y – 7 = 2(x – 2) ⇒ 2x – y + 3 = 0.

Question 26.
Find the absolute maximum value and minimum value of the following functions.

1. f(x) = 2x³ – 15x² + 36x + 1, x ∈ [1, 5]
2. f(x) = 12x^{\(\frac{4}{3}\)} – 6x^{\(\frac{1}{3}\)}, x ∈ [-1, 1]

Answer:
1. Given; f(x) = 2x³ – 15x² + 36x + 1, x ∈ [1, 5]
⇒ f'(x) = 6x² – 30x + 36
For turning point f'(x) = 0 ⇒ 6x² – 30x + 36 = 0
⇒ x² – 5x + 6 = 0 ⇒ (x -3)(x – 2) = 0
⇒ x = 3, 2
f(1) = 2(1)³ – 15(1)² + 36(1) + 1 = 24
f(2) = 2(2)³ – 15(2)² + 36(2) + 1 = 29
f(3) = 2(3)³ – 15(3)² + 36(3) + 1 = 28
f(5) = 2(5)³ – 15(5)² + 36(5) + 1 = 56
Absolute maximum = max {24, 29, 28, 56} = 56
Absolute minimum = min {24, 29, 28, 56} = 24

2. Given;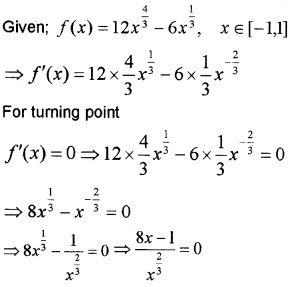

f'(x) = 0 at x = \(\frac{1}{8}\) and f'(x) is not defined at x = 0. Therefore;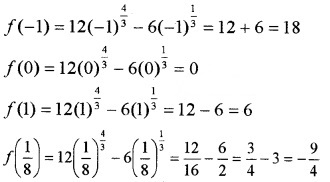

Absolute maximum = max {18, 0, 6, \(-\frac{9}{4}\)} = 18
Absolute minimum = min {18, 0, 6, \(-\frac{9}{4}\)} = \(-\frac{9}{4}\).

Question 27.
Consider the function y = x³ – 6x² + 3x – 1

1. Find the slope at x= -1. (1)
2. Find the minimum gradient of the above curve. (3)

Answer:
1. Given,
y = x³ – 6x² + 3x – 1 ⇒ y’ = 3x² – 12x + 3
Gradient at (x = -1) = (y’)_x=1 = 3(-1)² – 12(-1) + 3 = 18.

2. Now for minimum gradient we have to apply maxima – minima condition to the function y’ .ie, y” = 6x – 12 , for turning points of y’ is given by y” = 0.
Therefore, 6x – 12 = 0 ⇒ x = 2
Now, y”’ = 6 > 0
∴ y’ is maximum at x = 2.
Minimum gradient at (x = 2) is
= 12 – 24 + 3 = – 9.

Plus Two Maths Application of Derivatives Six Mark Questions and Answers

Question 1.
A curve passes through the origin, and its gradient function is 2x – \(\frac{x^{2}}{2}\)

1. Find its y coordinate when x= 2. (4)
2. Find the equation of the tangent at x= 2. (2)

Answer:
Given;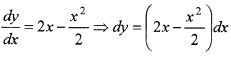

Integrating we have; ∫dy = ∫(2x – \(\frac{x^{2}}{2}\))dx
⇒ y = x² – \(\frac{x^{3}}{6}\) + c ___(1)
Since the curve passes through (0, 0)
(1) ⇒ 0 = 0 + c ⇒ c = 0
∴ Equation of the curve is y = x² – \(\frac{x^{3}}{6}\)
When x = 2 ⇒ y = 2² – \(\frac{2^{3}}{6}\) = \(\frac{8}{3}\)
∴ coordinate is (2, \(\frac{8}{3}\)).

2. Slope at (2, \(\frac{8}{3}\)) = 2 × 2 – \(\frac{2^{2}}{2}\) = 2
∴ Equation of the tangent at (2, \(\frac{8}{3}\)) is given by
y – \(\frac{8}{3}\) = 2(x – 2)
⇒ 3y – 8 = 6x – 12
⇒ 3y = 6x – 4.

Question 2.
(i) Choose the correct answer from the bracket. The slope of the tangent to the curve y = x³ – 2x + 3 at x = 1 is ____(1)
(a) 0
(b) 1
(c) 2
(d) 3
(ii) Find points on the curve \(\frac{x^{2}}{25}+\frac{y^{2}}{9}\) = 1 at which the tangents are (2)
(a) Parallel to x-axis
(b) parallel to the y-axis.
(iii) Use differential to approximate \(\sqrt{25.6}\). (3)
Answer:
(i) (b) 1, Since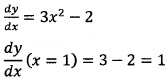

(ii)

(a) \(\frac{d y}{d x}\) = 0, since tangents are parallel to x- axis.
\(\frac{-9x}{25}\) = 0, x = 0 ∴ y = ± 3;
The points are (0, 3) and (0, -3)

(b) \(\frac{-25 y}{9 x}\) = 0, since tangents are parallel to y-axis, slope of normal = 0; y = o
∴ x = ± 5
The points are (5, 0) and (-5, 0)

(iii) Take y = \(\sqrt{x}\) , let x = 25 and ∆x = 0.6
Then; f(x) = y = \(\sqrt{x}\)
f(x + ∆x) = y + ∆y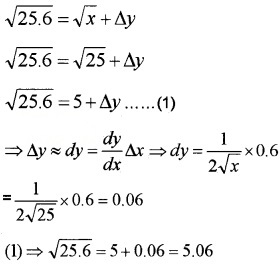

Question 3.
Let x and y be the length and breadth of the rectangle ABCD in a circle having radius r. Let ∠CAB = θ (Ref. figure). If ∆ represent area of the rectangle and r is a constant.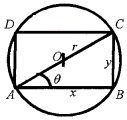

1. Write ∆ in terms of r and θ. (2)
2. Find \(\frac{d \Delta}{d \theta}\) and \(\frac{d^{2} \Delta}{d \theta^{2}}\). (1)
3. Hence find the maximum value of ∆. (2)
4. Show that the rectangle of maximum area that can be inscribed in a circle of radius r is a square of side \(\sqrt{2} r\). (1)

Answer:
1. Area of the rectangle is ∆ = xy
From the figure y = 2r sinθ, x = 2r cosθ
∆ = xy = 4r²sinθcosθ = 2r²sin2θ

2. \(\frac{d \Delta}{d \theta}\) = 4r² cos2θ ⇒ \(\frac{d^{2} \Delta}{d \theta^{2}}\) = -8r²sin2θ

3. For turning points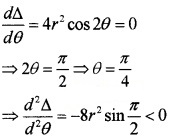

Therefore local maximum at θ = \(\frac{\pi}{4}\)

4. Then;

Hence the rectangle becomes a square.

Question 4.
The second derivative of the equation of a curve is given by the equation x \(\frac{d^{2} y}{d x^{2}}\) = 1, given y = 1, \(\frac{d y}{d x}\) = 0 when x= 1.

1. Find the slope at x = e. (2)
2. Find the equation of the curve. (2)
3. Find the equation of the normal at x= e. (2)

Answer:
1. Given;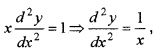

Integrating we get,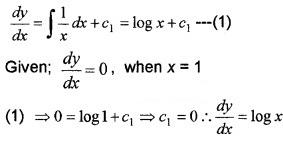

∴ Slope of the curve at x = e is given by
\(\left(\frac{d y}{d x}\right)_{x=e}\) = loge = 1.

2. We have,
\(\frac{d y}{d x}\) = logx, ⇒ dy = logxdx
Integrating we get,
∫dy = ∫logx dx ⇒ y = logx.x – ∫\(\frac{1}{x}\).x dx + c₂
⇒ y = xlogx – x + c₂ ____(2)
Given; y = 1 when x = 1
(2) ⇒ 1 = 1log1 – 1 + c₂ ⇒ 1 = 0 – 1 + c₂ ⇒ c₂ = 2
Therefore the equation of the curve is
y = xlogx – x + 2

3. We have, y = xlogx – x + 2
When x = e
⇒ y = e log e – e + 2 ⇒ y = e – e + 2 = 2
So we have to find the slope at (e, 2),
We know; \(\left(\frac{d y}{d x}\right)_{x=e}\) = log e = 1
∴ Slope of the normal at (e, 2)= -1
∴ Equation of the normal at (e, 2) is.
y – 2 = (-1) (x – e)
y – 2 = – x + e ⇒ y + x = e + 2.

Question 5.
The given figure represents a cylinder Inscribed in a sphere.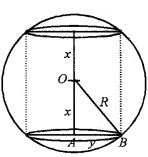

1. Find an expression for the volume V of the cylinder. (2)
2. Find the height of the cylinder when its volume V is maximum. (2)
3. Find the volume and radius of the largest cylinder. (2)

Answer:
1. From the right triangle ∆OAB,
y² = R² – x² ⇒ y = \(\sqrt{R^{2}-x^{2}}\)
Which is the radius of the cylinder
Also height = 2 x
∴ Volume = V= π y² × 2x = 2π(R² – x²)x = 2π(R²x – x³).

2. Now,

For maximum or minimum,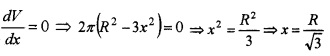

3. Base radius =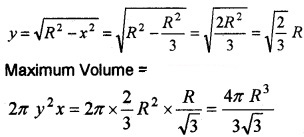

Question 6.
If f(x) = x³ + 3x² – 9x + 4 is a real function

1. Find the intervals in which the function is increasing or decreasing. (3)
2. Find the points of local maxima or local minima of f(x) (2)
3. Graph of a function is given in the following figure:

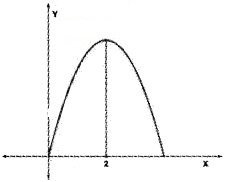
Which among the following represents the graph of its derivative? (1)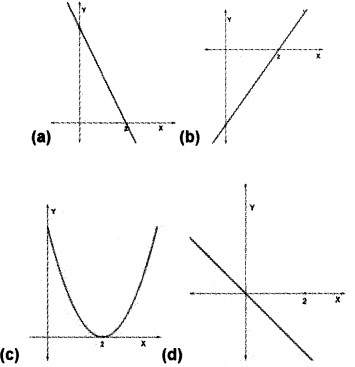

Answer:
1. f'(x) = 3x² + 6x – 9
For turning points f'(x) = 3x² + 6x – 9 = 0
⇒ x = 1, -3
These turning point divide the domain of f(x) in the following intervals. (-∞, -3), (-3, 1), (1, ∞) in (-∞, -3)
⇒ f'(-4) = 3(-4)² + 6(-4) – 9 > 0
Hence increasing.
In (-3, 1) ⇒ f'(0) = 3(0)² + 6(0) – 9 < 0
Hence decreasing.
In (1, ∞) ⇒ f'(2) = 3(2)² + 6(2) – 9 > 0
Hence increasing.

2. x = -3 is a local maximum point and x = 1 is a local minimum point.

3. (a)

The function passes through origin and has a local maximum at x = 2.

Question 7.
Of all the Cylinders with given surface area, show that the volume is maximum when height is equal to the diameter of the base.
Answer:
Let r be the radius, h be the height, V be the volume and S be the surface area
S = 2πr² + 2 πrh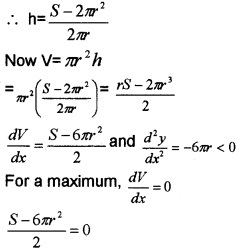

S – 6πr² = 0
2πr² + 2πrh – 6πr² = 0
So h = 2r
So volume is maximum when h = 2r.

Question 8.
Sand is pouring from a pipe. The falling sand forms a Cone on the ground in such a way that the height of the Cone is always one-sixth of the radius of the base.

1. Establish a relation between the volume ‘v’ and height ‘h’ of the Cone using the given condition. (2)
2. lf the sand is pouring at the rate of -12 cm/sec, Find the rate of change of height of the Cone. (2)
3. Find \(\frac{\mathrm{dh}}{\mathrm{dt}}\) when h = 4cm. (2)

Answer:
1. Given that the height of the Cone is one-sixth of the radius of the base, then h = \(\frac{r}{6}\) ⇒ r = 6h
Then Volume V = \(\frac{1}{3}\) πr²h = \(\frac{1}{3}\) π(6h)2.h
V = \(\frac{1}{3}\) π 36h².h = \(\frac{1}{3}\) π 36h³
V =12 πh³ ____(1)

2. Differentiating (1) we get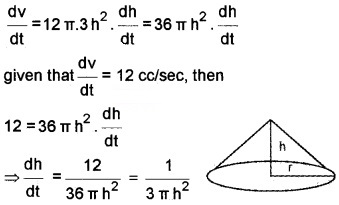

3. When h = 4 cm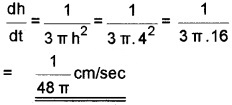

Question 9.
(i) Choose the correct answer from the bracket. The rate of change of the area of a circle with respect to its radius r at r = 10cm is.
(a) 10π
(b) 20π
(c) 30π
(d) 40π (1)
(ii) Find the intervals in which the function f given by f(x) = x² – 6x + 5 is (2)
(a) Strictly increasing
(b) Strictly decreasing
(iii) Find the local minimum and local maximum value, if any, of the function f(x) = x³ – 6x² + 9x + 8 (3)
Answer:

(ii) f'(x) = 2x — 6; 2x – 6 = 0; x = 3
(-∞, 3 ) is strictly decreasing
(3, ∞) is strictly increasing.

(iii) f'(x) = 3x² – 12x + 9
f¹¹ = 6x — 12
For maxima, minima
f¹ = 0 → 3x² – 12x + 9 = 0
3(x – 3)(x — 1) = 0; x = 3, x = 1
At x = 3 f¹¹(x) = 6 × 3 – 12 = 18 – 12 = 6 > 0
f is minimum, the local minimum value of f = 8
At x = 1 f¹¹(x) = 6 × 1 – 12 = -6 < 0,
f is maximum, the local maximum value of f = 12.

Question 10.
A wire of length 28m is cut into two pieces. One of the pieces is be made into a square and the other into a circle. What should be the length of the two pieces so that combined area of the square and the circle is minimum using differentiation?
Answer:
Let the length of one piece be ‘x’ and other piece be ‘28 – x’. Let from the first piece we will make a circle of radius Y and from the second piece we will make a square of side y. Then,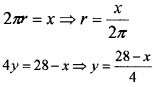

Let A be the combined area of the circle and square, then

Question 11.
An open box of the maximum volume is to be made from a square piece of tin sheet 24cm on a side by cutting equal squares from the corners and turning of the sides.
(i) Complete the following table. (2)

(ii) Using the above table, express V as a function of x and determine its domain. (1)
(iii) Find height (x. cm) of the box when volume V is maximum by differentiation. (3)
Answer:
(i)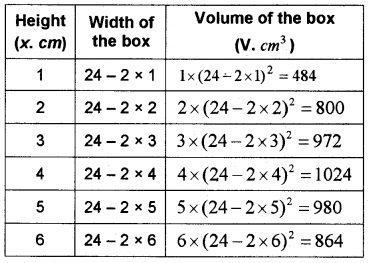

(ii) Generalise the above table as a function.
V = x(24-2x)², 0 < x < 12.

(iii) \(\frac{d V}{d x}\) = x.2(24 – 2x)(-2) + (24 – 2x)²
= -4x(24 – 2x) + (24 – 2x)²
= -96x + 8x² + 576 + 4x² – 96x
= 12x² – 192x + 576
For maximum or minimum,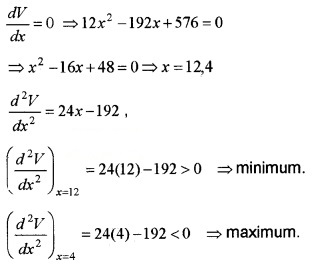

Therefore volume is maximum when x = 4 cm.

Question 12.
A square tank of capacity 250 m³ has to be dugout. The cost of land is Rs. 50 per m². The cost of digging increases with the depth and for the whole tank is Rs. 400 × (depth)².

1. Find an expression for the cost of digging the tank. (3)
2. Find the dimension of the tank when the total cost is least. (3)

Answer:
1. Let x, x and y be the length, breadth, and depth of the tank.
Then, V = x. x. y = 250 ⇒ y = \(\frac{250}{x^{2}}\).
Area of land = x²
⇒ Cost of land = 50 x²
(∵ cost of land is Rs.50/m²)
Cost of digging = 400 × (depth)² = 400 × (y)²
∴ Total cost = C = 50 x² + 400 × (y)²

2. We have, C = 50x² + \(\frac{400 \times(250)^{2}}{x^{4}}\).
Differentiating w.r.t.x, we get,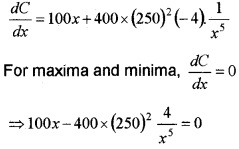


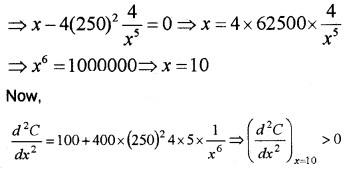
∴ Maximum at x = 10
m ⇒ when x = 10m and
y = \(\frac{250}{10^{2}}\) = 2.5m the total cost is least.

Question 13.
Show that the right circular cone of least curved surface and given volume has an altitude equal to \(\sqrt{2}\) times the radius of the base.
Answer:
Volume of the cone will be, V =\(\frac{1}{3}\)πr²h
h = \(\frac{3 V}{\pi r^{2}}\) ____(1)
Curved surface area will be, S = πrl
⇒ S² = π²r²l² = P
⇒ P = π²r²(h² + r²) ⇒ P = π²r²h² + π²r⁴)

⇒ 2r² = h² ⇒ h = \(\sqrt{2} r\).

Question 14.
Let ABC be an isosceles triangle inscribed in a circle having radius r. Then by figure, area of the triangle ABC is ∆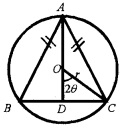

1. Find \(\frac{d \Delta}{d \theta}\) and \(\frac{d^{2} \Delta}{d \theta^{2}}\) (2)
2. Find the maximum value of ∆. (3)
3. Show that the isosceles triangle of maximum area that can be inscribed in a given circle is an equilateral triangle. (1)

Answer:
1. Area of the isosceles triangle is ∆ = \(\frac{1}{2}\)bh
From the figure b = r sin2θ, h = r + r cos2θ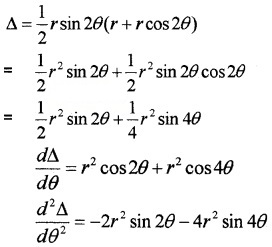

2. For turning points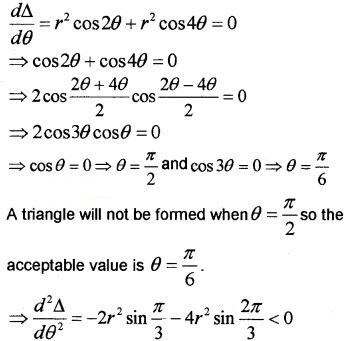

Therefore local maximum a θ = \(\frac{\pi}{6}\) which means the area of the isosceles triangle is maximum When θ = \(\frac{\pi}{6}\).

3. Then; ∠OCB = 30° ⇒ ∠ACB = 2∠OCB = 60°. Therefore the isosceles triangle is an equilateral triangle.

Question 15.
(i) Using the graph of the function f (x) in the interval [ a, h ] match the following.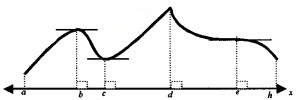

A – Point	B – Nature
x = a	Absolute maximum
x = b	Absolute minimum
x = e	Local maximum
x = d	Local minimum
Point of inflexion.

(ii) Consider the function f(x) = 3x⁴ – 8x³ + 12x² – 48x + 25
(a) Find the turning points of f(x). (1)
(b) Explain the nature of the turning points (1)
(c) Find the absolute extreme values of f(x). (2)
Answer:
(i)

A – Point	B – Nature
x = a	Absolute minimum
x = b	Local maximum
x = e	Point of inflexion
x = d	Absolute maximum

(ii) (a) f(x) = 12x³ – 24x² + 24x – 48
For turning points,
f'(x) = 0 ⇒ 12x³ – 24x² + 24x – 48 = 0
⇒ x³ – 2x² + 2x – 4 = 0
⇒ (x² + 2)(x – 2) = 0 ⇒ x = ± (\(\sqrt{-2}\), 2)
We admit only x = 2 as x = \(\sqrt{-2}\) is not a real number.
Therefore at x = 2 f (x) has a turning point.

(b) f”(x) = 36x² – 48x + 24
⇒ f”(2) = 36(2)² – 48 × 2 + 24 > 0
Therefore at x = 2 f(x) has a local minimum.

(c) f(0) = 25,
f(2) = 3(2)⁴ – 8(2)³ + 12(2)² – 48 × 2 + 25 = -39
f(3) = 3(3)⁴ – 8(3)³ + 12(3)² – 48 × 3 + 25 = 16
Consider the set { f (0), f{2), f (3)}
⇒ {25, -39, 16}
The maximum value of the above set is the absolute maximum and it is 25 at x = 0. The minimum value of the above set is the absolute minimum and it is -39 at x = 2.

Question 16.
An open box with a square base is to be made out of a given quantity of sheet of area a².

1. If the box has side x units, then show that volume V= \(\frac{a^{2} x-x^{3}}{4}\) (2)
2. Show that the maximum volume is \(\frac{a^{3}}{6 \sqrt{3}}\) (4)

Answer:
1. Area = a² = x² + 4xh,
h = height of the box.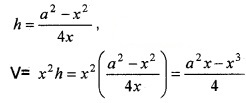

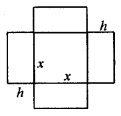
2. We have,

Question 17.
For the function f(x) = sin2x, 0 < x < π
(i) Find the point between 0 and π that satisfies f'(x) = 0. (2)
(ii) Find the point of local maxima and local minima. (2)
(iii) Find the local maximum and local minimum value. (2)
Answer:

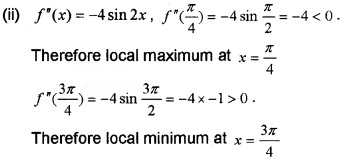
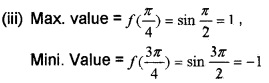
Question 18.
A cylindrical can with a volume of 125m3 (about 2 litres) is to be made by cutting its top and bottom from metal squares and forming its curved side by bending a rectangular sheet of metal to match its ends. What radius ‘r’ and height ‘h’ of the can will minimize the amount of material required.
Answer: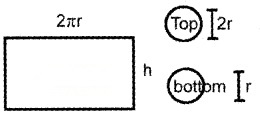

The circular top and bottom should be cut out from a square metal sheet of side 2r. Therefore the area of squares is 8r².
Area A = 8r² + 2πrh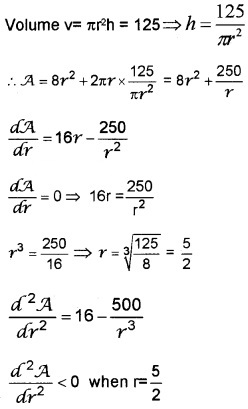

∴ To minimize the amount of material, r = 2.5
\(h=\frac{125}{\pi(2.5)^{2}}=6.3\).

Question 19.
A rectangle sheet of tin with adjascent sides 45cm and 24cm is to be made into a box • without top, by cutting off equal squares from the comers and folding up the flaps

1. Taking the side of the square cut off as x, express the volume of the box as the function of x. (2)
2. For what value of x, the volume of the box will be maximum. (4)

Answer:
1. Length of the box = 45 – 2x
Breadth of the box = 24 – 2x
Height of the box = x
Volume; V = (45 – 2x)(24 – 2x)x
= (1080 – 138x + 4x²)x
= 4x³ – 138x² + 1080x.

2. \(\frac{d y}{d x}\) = 12x² – 276x + 1080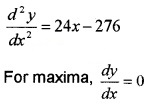

12x² – 276x + 1080 = 0
x² – 23x + 90 = 0
x = 18, 5
x = 18 is impossible
∴ x = 5 when x = 5, \(\frac{d^{2} y}{d x^{2}}\) < 0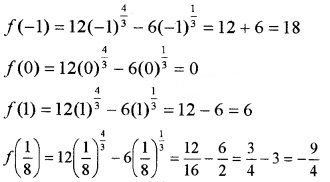

The volume of the box is maximum at x = 5.

Plus Two Mathematics All Chapters Question and Answers

• Plus Two Mathematics Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 1 Relations and Functions Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 2 Inverse Trigonometric Functions Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 3 Matrices Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 4 Determinants Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 5 Continuity and Differentiability Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 6 Application of Derivatives Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 7 Integrals Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 8 Application of Integrals Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 9 Differential Equations Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 10 Vector Algebra Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 11 Three Dimensional Geometry Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 12 Linear Programming Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 13 Probability Chapter Wise Question and Answers PDF

Benefits of the Plus Two Maths Chapter 6 Application of Derivatives Chapter Wise Question and Answers PDF

The Plus Two Maths Chapter 6 Application of Derivatives Chapter Wise Question and Answers PDF that has been provided above is extremely helpful for all students because of the way it has been drafted. It is designed by teachers who have over 10 years of experience in the field of education. These teachers use the help of all the past years’ question papers to create the perfect Plus Two Maths Chapter 6 Application of Derivatives Chapter Wise Question and Answers PDF.

FAQ’s Plus Two Maths Chapter 6 Application of Derivatives Chapter Wise Question and Answers PDF

Where can I download Plus Two Maths Chapter 6 Application of Derivatives Chapter Wise Question and Answers PDF?

You can download Plus Two Maths Chapter 6 Application of Derivatives Chapter Wise Question and Answers PDF for the latest 2021 session.

Can I download Plus Two All subjects Question and Answers PDF?

Yes - You can click on the links above and download subject wise question papers in PDF

Is there any charge for the Plus Two Maths Chapter 6 Application of Derivatives Chapter Wise Question and Answers PDF?

There is no charge for the model papers for you can download everything free